Найдем корни знаменателя, т.е. найдем значение x при которых функция будет не определена. Это и будут точки разрыва функции.
$$x^2+5x+6=0 =>x_{1,2}=\frac{-5 \pm \sqrt{25-4*6}}{2} => x_1=-2;x_2=-3$$
Рассмотрим поведение функции справа и слева от этих точек
Рассмотрим поведение функции в окрестности точки x=-2
Найдем левосторонний предел $$\lim_{x \to -2 -0} \frac{x+2}{|x^2+5x+6|} =\lim_{x \to -2 - 0} \frac{x+2}{|(x+2)(x+3)|}$$ В пределе нужно раскрыть модуль. Т.к. в окрестности точки x=-2 слева x+2 < 0, а x+3 > 0, т.е. модуль отрицательный, то согласно правила раскрытия модуля получим |(x+2)(x+3)|=-(x+2)(x+3). Подставляем в предел и получаем $$\lim_{x \to -2 -0} \frac{x+2}{|(x+2)(x+3)|}=\lim_{x \to -2 -0} \frac{x+2}{-(x+2)(x+3)}=\lim_{x \to -2 -0} \frac{1}{-(x+3)}=-1$$
Найдем правосторонний предел $$\lim_{x \to -2 +0} \frac{x+2}{|x^2+5x+6|} =\lim_{x \to -2 +0} \frac{x+2}{|(x+2)(x+3)|}$$ В пределе нужно раскрыть модуль. Т.к. в окрестности точки x=-2 справа x+2 > 0, а x+3 > 0, т.е. модуль положительный, то согласно правила раскрытия модуля получим |(x+2)(x+3)|=(x+2)(x+3). Подставляем в предел и получаем $$\lim_{x \to -2 +0} \frac{x+2}{|(x+2)(x+3)|}=\lim_{x \to -2 +0} \frac{x+2}{(x+2)(x+3)}=\lim_{x \to -2 +0} \frac{1}{x+3}=1$$
Получили $$\lim_{x \to -2-0} \frac{x+2}{|x^2+5x+6|} \ne \lim_{x \to -2+0} \frac{x+2}{|x^2+5x+6|}$$
Вывод: точка \(x=-2\) - точка разрыва первого рода
Рассмотрим поведение функции в окрестности точки x=-3
Найдем левосторонний предел $$\lim_{x \to -3 -0} \frac{x+2}{|x^2+5x+6|} =\lim_{x \to -3 - 0} \frac{x+2}{|(x+2)(x+3)|}$$ В пределе нужно раскрыть модуль. Т.к. в окрестности точки x=-3 слева x+2 < 0, а x+3 < 0, т.е. модуль положительный, то согласно правила раскрытия модуля получим |(x+2)(x+3)|=(x+2)(x+3). Подставляем в предел и получаем $$\lim_{x \to -3 -0} \frac{x+2}{|(x+2)(x+3)|}=\lim_{x \to -3 -0} \frac{x+2}{(x+2)(x+3)}=\lim_{x \to -3 -0} \frac{1}{x+3}=-\infty$$
Найдем правосторонний предел $$\lim_{x \to -3 +0} \frac{x+2}{|x^2+5x+6|} =\lim_{x \to -3 +0} \frac{x+2}{|(x+2)(x+3)|}$$ В пределе нужно раскрыть модуль. Т.к. в окрестности точки x=-3 справа x+2 < 0, а x+3 > 0, т.е. модуль отрицательный, то согласно правила раскрытия модуля получим |(x+2)(x+3)|=-(x+2)(x+3). Подставляем в предел и получаем $$\lim_{x \to -3 +0} \frac{x+2}{|(x+2)(x+3)|}=\lim_{x \to -3 +0} \frac{x+2}{-(x+2)(x+3)}=\lim_{x \to -3 +0} \frac{1}{-(x+3)}=-\infty$$
Получили $$\lim_{x \to -3-0} \frac{x+2}{|x^2+5x+6|} = -\infty ; \quad \lim_{x \to -3+0} \frac{x+2}{|x^2+5x+6|}=-\infty$$
Вывод: точка \(x=-3\) - точка разрыва второго рода, в этой точке функция имеет бесконечный скачек.
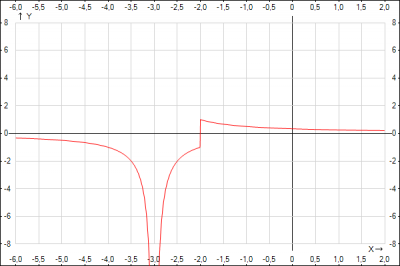
На рисунке изображен график функции $$f(x)=\frac{x+2}{|x^2+5x+6|}$$ для проверки на истинность рассуждений