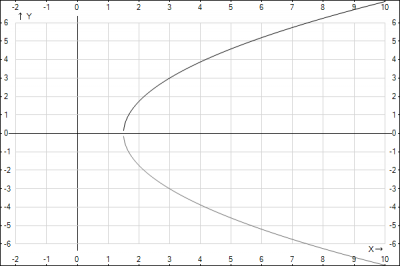
Согласно определения: парабола - геометрическим местом точек, равноудаленных от точки, которая называется фокусом и заданной прямой, которая называется директрисой. Т.е. нам необходимо найти уравнение параболы с фокусом в т. F(3;0) и директрисой - осью Oy. Как мы помним уравнение параболы имеет вид $$y^2=2px$$ Из условия мы можем найти параметр \(p=3\) - расстояние от фокуса до директрисы (оси Oy). Точка пересечения параболы с осью Ox находится в т. \(x=\frac{3}{2}\), по середине между директрисой и фокусом, т.е. парабола смещена в право по оси Ox на \(\frac{3}{2}\), т.е. уравнение параболы будет иметь вид $$y^2=2p(x-x_0)$$ Подставляем полученные данные и получаем уравнение параболы $$y^2=2*3(x-\frac{3}{2}) =>$$$$y^2=6(x-\frac{3}{2})$$Построим параболу и убедимся в правильности решения.