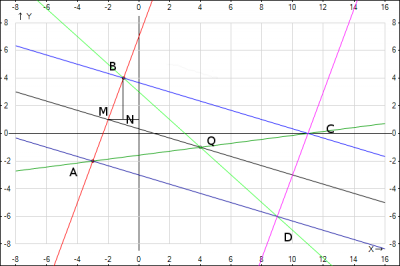
Найдем координаты вершин точек A и B, а затем применим формулу прямой, проходящей через две заданные точки. Это и будут искомые уравнения диагоналей прямоугольника.
Приступаем: Опустим перпендикуляр на сторону AB а точку M. Согласно свойства прямоугольника BC = 2QM => QM=AB, а т.к. перпендикуляр является медианой равнобедренного треугольника ΔABQ, то AB=2MB, т.е. если мы найдем высоту, то мы найдем и длину одной стороны прямоугольника.
Длину высоты будем искать по формуле расстояния от точки до прямой $$s = \frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}$$ Уравнение прямой AB известно \(3x-y+7=0\), координаты точки Q(4;-1), подставляем и находим $$QM=\frac{3*4+1+7}{\sqrt{9+1}} = \frac{20}{\sqrt{10}}$$Мы помним, что $$AM=MB= \frac{1}{2}QM=>AM=MB= \frac{1}{2} \frac{20}{\sqrt{10}}=\sqrt{10}$$Для нахождения координат точек A и B длины стороны не достаточно. Нужно привязаться к координатам. Можем найти координаты точки M. Для этого найдем уравнение прямой MQ, а затем точку пересечения MQ и AB - координаты точки M.
Нахождение уравнения прямой MQ. Известно, что эта прямая перпендикулярна прямой AB, на основании свойства угловых коэффициентов перпендикулярных прямых \(k_1=-\frac{1}{k_2}\) получим угловой коэффициент \(k_{MQ} = -\frac{1}{k_{AB}} = -\frac{1}{3}\). А теперь применим формулу прямой, проходящей через заданную точку в заданном направлении \(y-y_o=k(x-x_0)\), получим уравнение MQ $$y+1=-\frac{1}{3}(x-4) =>y=-\frac{1}{3}x+\frac{1}{3}$$
Нахождение точек пересечения прямых MQ и AB - координаты точки M. Составим систему уравнение $$\begin{cases}y=-\frac{1}{3}x+\frac{1}{3}\\3x-y+7=0 \end{cases}=>
\begin{cases}3x+7=-\frac{1}{3}x+\frac{1}{3}\\y=3x+7 \end{cases}=>$$$$\begin{cases}9x+21=-x+1\\y=3x+7 \end{cases}=>\begin{cases}x=-2\\y=1 \end{cases}$$ Получили координаты точки M(-2;1).
Нахождение координат вершин A и B. Построим ΔMBN. Из точки B проводим прямую параллельную оси Oy, а из точки M параллельно оси Ox. Это было сделано, чтобы получить угол BMN, который известен \(tg BMN = k_{AB}=3 =\frac{BN}{MN} => BN=3MN\). Т.к. треугольник ΔMBN прямоугольный и у него известна гипотенуза \(MB =\sqrt{10}\), а о катетах известно, что BN=3MN, по теореме Пифагора получим $$BN^2+MN^2=MB^2 =>9MN^2+MN^2=10=>MN=1 => BN=3$$ Ну а теперь можно просто найти координаты вершин A и B. Из рисунка видно что вершина B находится правее и выше вершины M, получим B(-2+1;1+3) =>B(-1;4), а вершина A находится левее вниз, т.е. A(-2-1;1-3) =>A(-3;-2)
Нахождение уравнений диагоналей прямоугольника: для обеих диагоналей у нас есть две точки, чтобы получить уравнение прямых воспользуемся формулой прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек A(-3;-2) и Q(4;-1), получаем уравнение диагонали AQ $$\frac{x+3}{4+3}=\frac{y+2}{-1+2} =>y = \frac{1}{7}x-\frac{11}{7}$$ Подставляем координаты точек B(-1;4) и Q(4;-1), получаем уравнение диагонали BQ $$\frac{x+1}{4+1}=\frac{y-4}{-1-4} =>y = -x+3$$
Нахождение уравнений сторон BC и AD прямоугольника: уравнения этих прямых найдем следующим образом: по известной координате вершины и угловому коэффициенту который равен угловому коэффициенту прямой MQ, т.к. они параллельные \(k=-\frac{1}{3}\). Подставляем данные в уравнение прямой, проходящей через заданную точку в заданном направлении \(y-y_0=k(x-x_0)\) и получаем для прямой BC с известной координатой точки B(-1;4) $$y-4=-\frac{1}{3}(x+1) =>y=-\frac{1}{3}x+\frac{11}{3}$$для прямой AD с известной координатой точки A(-3;-2) $$y+2=-\frac{1}{3}(x+3) =>y=-\frac{1}{3}x-3$$
Нахождение уравнения сторон DС прямоугольника: найдем координаты точки C как точки пересечения прямой BC и оси Ox, т.е. в этой точке y=0. Подставляем в уравнение прямой BC и находим x \(y=-\frac{1}{3}x+\frac{11}{3} =0 =>x=11\). Координаты точки C(11;0). Угловой коэффициент прямой DC известен он равен угловому коэффициенту прямой AB как две параллельные прямые \(k=3\). Подставляем в уравнение прямой, проходящей через заданную точку C(11;0) в заданном направлении \(k=3\), получаем $$y-0=3(x-11) => y=3x-33$$
Нанесем все прямые и точки на рисунок