По уравнению кривой 2-го порядка $4x^2-9y^2-16x-18y-29=0$ определить: тип кривой, привести уравнен

Дополним уравнение второго порядка до полных квадратов по x и y.

$$4x^2-9y^2-16x-18y-29=0 => (4x^2-16x)-(9y^2+18y)-29=0$$ $$4(x^2-4x)-9(y^2+2y)-29=0 =>$$ $$4*(x^2-2*x*2+4-4)-9(y^2+2*y*1+1-1)-29=0 =>$$ $$4*((x-2)^2-4)-9((y+1)^2-1)-29=0=>$$ $$4(x-2)^2-16-9(y+1)^2+9-29 =0 =>4(x-2)^2-9(y+1)^2-36 =0$$ Перенесем свободный член в правую часть уравнения и разделим обе части уравнения на него $$4(x-2)^2-9(y+1)^2=36=> \frac{(x-2)^2}{9}-\frac{(y+1)^2}{4}=1$$ Получили уравнение гиперболы в каноническом виде $$\frac{(x-2)^2}{3^2}-\frac{(y+1)^2}{2^2}=1$$ где $a=3$ - действительная полуось, т.е. гипербола имеет точки пересечения с осью Ох. Проверяем, подставляем в уравнение $y=0$, получаем точки пересечения с осью Ox  $x=\pm\frac{3}{2}\sqrt5+2 => x_1 \approx -1.35; \quad x_2 \approx 5.35$
$b=2$ - мнимая полуось.
Центр гиперболы расположен в точке $O(2;-1)$.

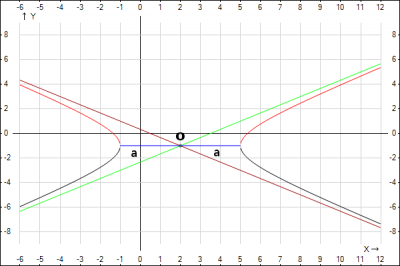
Найдем уравнения асимптот гиперболы $$\frac{x-x_0}{a} \pm \frac{y-y_0}{b} =0$$   Подставим значения полуосей, центра и получим $$\frac{x-2}{3} \pm \frac{y+1}{2} =0 =>\left[\begin{array}{c}y= -\frac{2}{3}x+ \frac{1}{3}\\ y= \frac{2}{3}x- \frac{7}{3}\end{array}\right.$$ получили уравнения асимптот. Теперь можно и построить график гиперболы.