Нам нужно найти координаты точки принадлежащей графику функции расстояние от которой до т. M будет наименьшим. Расстояние между двумя точками на плоскости рассчитывается по следующей формуле: $$S= \sqrt{(x-x_0)^2+(y-y_0)^2}$$где \((x_0;y_0)\) - это координаты точки M(-2;0), а \((x;y)\) -координаты точки, которая принадлежит графику функции, которую нужно найти. Подставим известные координаты в уравнение $$S = \sqrt{(x+2)^2+(y-0)^2}$$
В задании стоит слово наименьшее, это уже указывает на необходимость поиска экстремумов, т.е. нужно найти точку минимума функции \(S(x;y)\), т.е. нудно найти первую производную от расстояния S между точками и приравнять ее к нулю \(S'=0\). В уравнении x и y принадлежат графику функции, поэтому выразим y через x $$S = \sqrt{(x+2)^2+(-\sqrt{2-x})^2} = \sqrt{(x+2)^2+2-x}$$теперь найдем производную и приравняем ее к нулю. $$S' = (\sqrt{(x+2)^2+2-x})' = \frac{2(x+2)-1}{2*\sqrt{(x+2)^2+2-x}} =0$$Дробь будет равна нулю, если числитель равен нулю $$2(x+2)-1=0 =>2x+4-1=0=>x=-\frac{3}{2}$$ Получили координату x, подставляем ее в уравнение графика функции и получаем \(y = -\sqrt{2-x} = -\sqrt{2 +\frac{3}{2}} = -\sqrt{\frac{7}{2}}\). Получили координаты точки \(N(-\frac{3}{2};-\sqrt{\frac{7}{2}})\) - это и будет искомая точка. Для полноты расчетов необходимо проверить, является ли эта точка точкой минимума, подставим значение x левее и правее точки минимума в производную и проверим знак производной:
S'(-3) < 0
S'(0) > 0, т.е. найденная нами точка \(N(-\frac{3}{2};-\sqrt{\frac{7}{2}})\) - точка минимума.
Получим искомое расстояние, подставив координаты этой точки в формулу расстояния $$S_{min} = \sqrt{(x+2)^2+y^2} = \sqrt{(-\frac{3}{2}+2)^2+\frac{7}{2}}=\sqrt{\frac{1}{4}+\frac{7}{2}} = \frac{\sqrt{15}}{2}$$ Наименьшее расстояние между точкой и кривой \(S=\frac{\sqrt{15}}{2}\)
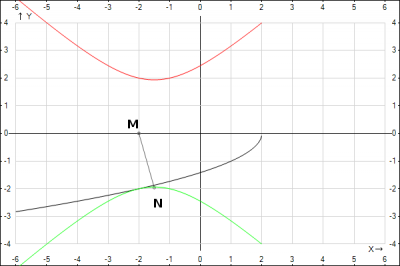
На рисунке график функции:
\(y = -\sqrt{2-x}\) - черным
\(S = \sqrt{(x+2)^2+2-x}\) - красным
\(S_1 = -\sqrt{(x+2)^2+2-x}\) - зеленым - симметричное отображение графика расстояния относительно от Ox для наглядности \(S=|S_1|\).