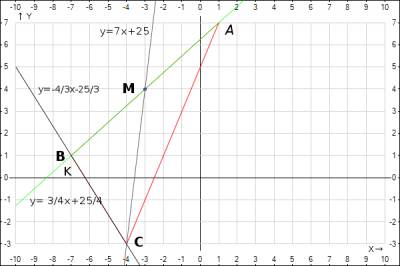
1. Найдем уравнение стороны BC.
В условии даны координаты вершин B и C, поэтому воспользуемся уравнением прямой, проходящей через две точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$ Подставим координаты это уравнение $$\frac{x-(-7)}{-4-(-7)}=\frac{y-1}{-3-1} => y = -\frac{4}{3}x-\frac{25}{3}$$
2.Уравнение высоты АК и ее длину
Прямая AK - прямая перпендикулярная прямой BC. Известно свойство перпендикулярных прямых \(k_1=-\frac{1}{k_2}\). Угловой коэффициент прямой BC известен и равен \(k_{BC}=-\frac{4}{3}\), тогда угловой коэффициент прямой AK равен \(k_{AK} =-\frac{1}{k_{BC}} = -\frac{1}{-\frac{4}{3}} = \frac{3}{4}\). О прямой AK у нас известно, что она проходит через точку A и имеет угловой коэффициент \(k_{AK}=\frac{3}{4}\). Воспользуемся уравнением прямой, проходящей через точку в заданном направлении $$y-y_0=k*(x-x_0)$$ Подставим координаты точки и угловой коэффициент $$y-7=\frac{3}{4}*(x-1) => y = \frac{3}{4}x+\frac{25}{4}$$Длина высоты - расстояние от точки до прямой. Расстояние рассчитывается по формуле $$d= \frac{|Ax_0+Bx_0+C|}{\sqrt{A^2+B^2}}$$Т.е. у нас есть уравнение прямой BC, подставляем в него координаты точки A, предварительно, для удобства расчетов приведем это уравнение к каноническому виду \(y = -\frac{4}{3}x-\frac{25}{3} =>4x+3y+25=0\) Подставляем в уравнение расстояния $$AK = \frac{|4*1+3*7+25|}{\sqrt{16+9}} = \frac{50}{5}=10$$
3.Уравнение медианы СМ.
Медиана CM проходит через середину отрезка AB. Координаты точек A и B известны, поэтому найдем координату точки \(M(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}) => M(\frac{1-7}{2};\frac{7+1}{2})\) =>\(M(-3;4)\). Получили, что медиана проходит через две C и M точки с известными координатами, поэтому для получения уравнения медианы воспользуемся уравнением прямой, проходящей через две точки. $$\frac{x-(-3)}{-4-(-3)}=\frac{y-4}{-3-4} =>y = 7x+25$$
4.Площадь этого треугольника
Найдем площадь треугольника ABC. $$S=\frac{1}{2}a*h$$ У нас известна высота \(AK=10\), нужно найти длину отрезка \(BC\), находим $$BC = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} = \sqrt{(-7-1)^2+(1-7)^2} = \sqrt{64+36}=10$$Подставляем в формулу площади и получаем $$S_{ABC} = \frac{1}{2}*10*10=50$$
Нанесем полученные прямые и точки на рисунок.
Треугольник ABC оказался прямоугольным, а прямые AK и AB совпали.