Найти плотность распределения, функцию распределения, построить их графики.
Согласно определения: случайная величина имеет непрерывное распределение на отрезке [a;b], если ее плотность имеет вид: $$f(x) = \begin{cases}\frac{1}{b-a}, \forall x \in [a;b] \\0 , \forall x \ne [a;b] \end{cases}$$
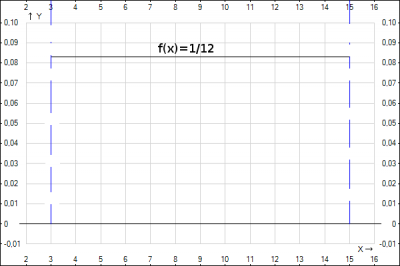
В нашей задаче плотность распределения будет иметь вид $$f(x) = \begin{cases}\frac{1}{15-3}, \forall x \in [3;15] \\0 , \forall x \ne [3;15] \end{cases} =>f(x) = \begin{cases}\frac{1}{12}, \forall x \in [3;15] \\0 , \forall x \ne [3;15] \end{cases}$$
График плотности распределения
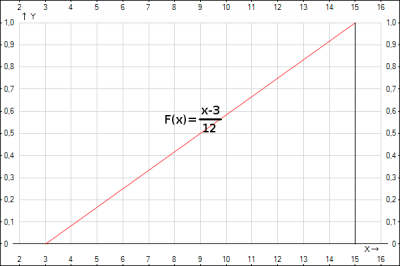
Согласно определения плотности распределения: предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от x до x+Δx к длине этого участка Δx, когда Δx стремится к 0, называется плотностью распределения $$\lim_{Δx \to 0}\frac{F(x+Δx)-F(x)}{Δx}=f(x) = F'(x)$$ Это определение я привел для того, чтобы вспомнить, что $$f(x) = F'(x)$$ т.е. плотность распределения равна производной от функции распределения, т.е. $$F(x) =\int_a^bf(x)dx$$ Подставляем и находим функцию распределения $$F(x) =\begin{cases} 0, x < a \\ \frac{x-3}{12}, x \in [3;15] \\ 1, x > 15 \end{cases}$$ для точек отрезка [a;b] интеграл равен \(F(x) = \int_3^x \frac{1}{12}dx = \frac{1}{12}x|_3^x=\frac{x-3}{12}\)
График функции распределения
Найти вероятность попадания случайной величины в интервал (6, 11)
Функцию распределения мы уже нашли. Подставим граница интервала это и будет искомая вероятность $$P=\frac{x-3}{12}|_6^{11}= \frac{11-3}{12} - \frac{6-3}{12} =\frac{5}{11}$$
Можно было просто найти площадь прямоугольника ограниченного кривой плотности распределения - это одна сторона прямоугольника \(a = f(x) = \frac{1}{12}\) и длиной заданного интервала это будет вторая сторона прямоугольника \(b = 11-6=5\), тогда площадь, которая равна вероятности будет равна \(S=P=a*b=\frac{5}{12}\)
Найти математическое ожидание, дисперсию и среднеквадратичное отклонение.
Математическое ожидание равно $$M_x = \frac{a+b}{2} = \frac{3+15}{2}=9$$
Дисперсия равна $$D_x=\frac{(b-a)^2}{12} = \frac{(15-3)^2}{12}=12$$



