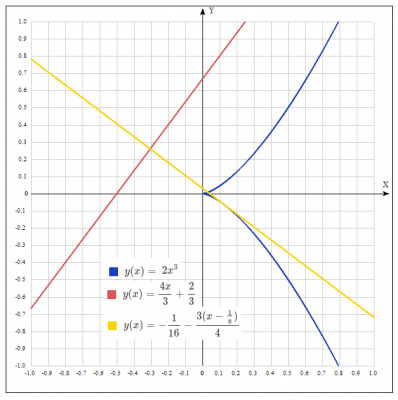
В какой точке кривой \(y^2= 2x^3\) касательная перпендикулярна прямой \(4x- 3y+2 =0\)
Решение: вспомним уравнение касательной: \(y = f(x_0)+f'(x_0)(x-x_0)\). Из условия задачи следует, что нам нужно найти координаты точки \((x_0;y_0)\) при условии, что касательная перпендикулярна прямой \(4x- 3y+2 =0\).
Воспользуемся геометрическим смыслом производной.
Геометрический смысл производной. Производная в точке \(x_0\) равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Обозначим угловой коэффициент \(k_1 = f'(x_0)\)
Из условия известно, что касательная \(y = f(x_0)+f'(x_0)(x-x_0)\) в точке касания \((x_0;y_0)\) перпендикулярна прямой \(4x- 3y+2 =0 \quad (1)\). Приведем уравнение прямой (1) к виду - уравнения прямой с угловым коэффициентом \(y = kx+b\), где k - угловой коэффициент прямой, b – некоторое действительное число. $$4x- 3y+2 =0 => y = \frac{4}{3}+\frac{2}{3} \quad (2)$$ Обозначим угловой коэффициент примой \(k_2= \frac{4}{3}\).
Из условия известно, что прямая и касательная перпендикулярны.
Воспользуемся свойством перпендикулярных прямых:
Прямые \(y=k_1x+b_1 \quad y = k_2x+b_2\) перпендикулярны, если \(k_1*k_2=-1\).
Подставляем значение \(k_2\) и получаем \(k_1\)
$$k_1*\frac{4}{3} = -1 =>k_1 = -\frac{3}{4} => f'(x_0) = -\frac{3}{4}$$ Для нахождения координат точки составим систему из двух уравнений
1. \(y_0^2= 2x_0^3\) - точка касания принадлежит кривой.
2. для получания второго уравнения применим формулу \(y' = f'(x_0) = -\frac{3}{4}\) - угловой коэффициент касательной в точкее касания.
Найдем производную функции \(y^2= 2x^3\). $$(y^2)'= (2x^3)' => 2y*y' = 6x^2 => y*y' = 3x^2$$ Получили второе уравнение в точке \((x_0;y_0)\) $$ y_0*y'_0 = 3x_0^2$$ подставляем значение \(f'(x_0) = -\frac{3}{4}\), получаем $$ y_0*(-\frac{3}{4}) = 3x_0^2 => -y_0 = 4x_0^2$$ Получили, что при решении системы уравнений мы должны выбрать только отрецательные решения \(y_0\).
Строим систему: $$\begin{cases}y_0^2= 2x_0^3\\-y_0 = 4x_0^2\end{cases} => \begin{cases}16x_0^4= 2x_0^3\\y_0 = -4x_0^2\end{cases}=> \begin{cases} x_0= \frac{1}{8}\\ y_0 = -\frac{1}{16}\end{cases}$$
Ответ: координаты искомой точки \((\frac{1}{8}; -\frac{1}{16})\)
Построим кривые и проверим решение графическим методом.