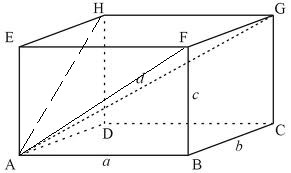
Рассмотрим прямоугольный параллелепипед ABCDEHGF (рис.). Обозначим стороны AB=a; DC=b; BF=c. Углы α,β, γ - углы между диагональю AG=d и ее проекцией на грани ABCD - \(\alpha = \angle GAC\), AEFB - \(\beta = \angle FAG \), AEHD - \( \gamma = \angle HAG\).
Докажем следующее равенство $$\sin^2\alpha + \sin^2 \beta + \sin^2 \gamma = 1 \quad$$
В задаче говорится о синуса в квадрате, поэтому целесообразно использовать в доказательстве теорему Пифагора.
Рассмотрим треугольник \(ΔGAC\). В этом треугольнике \(\sin \alpha = \frac{c}{d}\).
Рассмотрим треугольник \(ΔFAG\). В этом треугольнике \(\sin \beta = \frac{b}{d}\).
Рассмотрим треугольник \(ΔHAG\). В этом треугольнике \(\sin \gamma = \frac{a}{d}\).
В этих формулах присутствует d - длина диагонали. Найдем ее : из прямоугольного треугольника \(ΔABC\) по теореме Пифагора находим \(AC^2 = AB^2+BC^2 = a^2+b^2\). Из прямоугольного треугольника \(ΔGAC\) по теореме Пифагора находим \(AG^2 = AC^2 + CG^2 = a^2+b^2+c^2 => d^2 = a^2+b^2+c^2 \).
Подставим полученные данные в (2) $$\sin^2\alpha + \sin^2 \beta + \sin^2 \gamma = (\frac{c}{d})^2+(\frac{b}{d})^2+(\frac{a}{d})^2 = \frac{c^2}{a^2+b^2+c^2}+\frac{b^2}{a^2+b^2+c^2}+\frac{a^2}{a^2+b^2+c^2} = \frac{a^2+b^2+c^2}{a^2+b^2+c^2}=1$$ Равенство доказано.



