Рассмотрим рисунок:
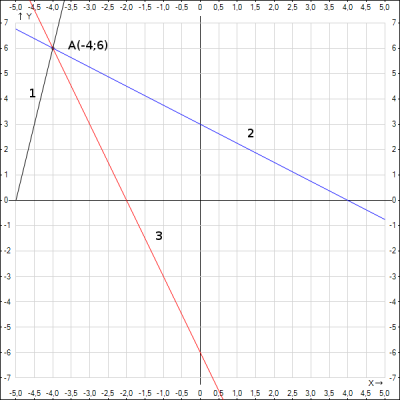
Через точку \(A\) можно провести всего 3 прямые, которые бы отсекали на осях отрезки, которые будут катетами искомого треугольника. У нас в задании известна точка через которую проходят эти прямые, поэтому воспользуемся уравнением прямой, проходящей через одну точку в заданном направлении: $$y-y_0 = k(x - x_0) $$где \(x_0;y_0\) - координаты известной точки \(A(-4;6)\). Подставим координаты в уравнение, получим $$y - 6 = k(x +4)$$Это уравнение трех прямых, проходящих через одну точку. Учтем еще один факт. У прямой \(1\) положительный угловой коэффициент \(k >0\), а у прямых \(2;3\) - отрицательный, т.к. угол наклона с положительным направлением оси \(Ox\) больше \(90^0\). Отразим это в уравнении прямых \(2;3\) $$y - 6 = - k(x +4)$$ Катетами треугольников являются отрезки на осях, отсекаемые этими прямыми, поэтому площадь треугольника (треугольник прямоугольный) можно представить в следующем виде $$S = \frac{1}{2}X_{y=0}*Y_{x=0}$$где
\(X_{y=0}\) - значение \(|x|\) в точке пересечения прямой с осью \(Ox\), т.е. при \(y =0\),
\(Y_{x=0}\) - значение \(|y|\) в точке пересечения прямой с осью \(Oy\), т.е. при \(x =0\)
Рассмотрим два случая:
1. прямая \(1\). Найдем значение точек пересечения с осями
$$y - 6 = k(x +4) =>\begin{cases}x=0 &|& Y_{x=0} = k(0+4)+6\\y =0 &|& 0 = k(X_{y=0}+4)+6 \end{cases}=>$$$$\begin{cases}Y_{x=0} = 4k+6\\X_{y=0}= |-\frac{6}{k}-4|\end{cases}=>
\begin{cases}Y_{x=0} = 4k+6\\X_{y=0}= \frac{6}{k}+4\end{cases}$$Мы получили зависимость длин катетов от одного неизвестного \(k\) - углового коэффициента прямой. Подставим полученные значения длин катетов в формулу площади и найдем неизвестную \(k\) $$S = \frac{1}{2}X_{y=0}*Y_{x=0} => 6 = \frac{1}{2}(\frac{6}{k}+4)(4k+6) =>$$$$(4k+6)^2=12k =>(2k+3)^2=3k =>4k^2+12k+9 = 3k =>$$$$4k^2+9k+9 = 0 => k_{1,2} = \frac{-9 \pm \sqrt{81-4*4*9}}{8}$$Получили дискриминант меньше 0, оно и понятно, из рисунка видно, как бы мы не провели прямую \(1\) площадь будет больше 6.
2. прямые \(2;3\). Найдем значение точек пересечения с осями
$$y - 6 = -k(x +4) =>\begin{cases}x=0 &|& Y_{x=0} = -k(0+4)+6\\y =0 &|& 0 = -k(X_{y=0}+4)+6 \end{cases}=>$$$$\begin{cases}Y_{x=0} = -4k+6\\X_{y=0}= \frac{6}{k}-4\end{cases}
$$Мы получили зависимость длин катетов от одного неизвестного \(k\) - углового коэффициента прямой. При этом обращаю внимание, что координаты точек пересечения или обе положительные или обе отрицательные, т.е. площадь треугольника всегда будет положительной, поэтому по модулю значения \(x;y\) можно не брать. Подставим полученные значения длин катетов в формулу площади и найдем неизвестную \(k\) $$S = \frac{1}{2}X_{y=0}*Y_{x=0} => 6 = \frac{1}{2}(-4k+6)( \frac{6}{k}-4) =>$$$$(6 -4k)^2=12k =>(3- 2k)^2=3k =>4k^2-12k+9 = 3k =>$$$$4k^2-15k+9 = 0 => k_1,2 = \frac{15 \pm \sqrt{225-4*4*9}}{8} =\frac{15 \pm 9}{8} =>$$$$\left[\begin{array}{c}k_1 = 3\\ k_2 =\frac{3}{4}\end{array}\right.$$Подставляем \(k_1;k_2\) в уравнение прямых \(2;3\) и получаем два уравнения прямых$$ \begin{array}{c}y - 6 = -3(x +4) \\ y - 6 = -\frac{3}{4}(x +4) \end{array}=>\begin{array}{c}y = -3x -6 \quad (3)\\ y = -\frac{3}{4}x +3 \quad (2)\end{array}$$Ответ: уравнение прямых, проходящих через заданную точку, образующие с отрезками на осях треугольник с заданной площадью равны $$\begin{array}{c}y = -3x -6 \quad (3)\\ y = -\frac{3}{4}x +3 \quad (2)\end{array}$$



