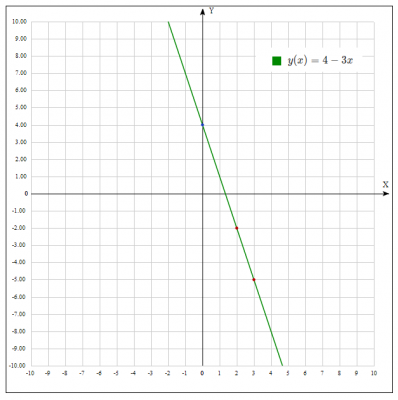
Решение: в задании даны две точки, через которые проходит прямая. Уравнения этой прямой будем искать при помощи формулы уравнения прямой, проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \)
Подставляем координаты точек A(2,−2) и B2(3,−5): $$ \frac{x-2}{3-2} = \frac{y+2}{-5+2} => y = 4-3x$$
Найдем точку переечения этой прямой и оси Oy. Первая координата точки пересечения \(x=0\) Подставляем в уравнение прямой $$y(0) = 4-3*0 = 4 $$
Ответ: координаты точки пересечения прямой и оси Oy \((0;4)\)