Решение: дано уравнение кривой \(z = \frac{4}{x^2} \quad ; y= 0\)
1. Составим уравнение поверхности, образованной вращением линии вокруг оси Oz.
В задании дано уравнение, которое можно рассматривать как проекция фигуры вращения на плоскость zOx, т.е. при y=0.
Т.к. это фигура вращения, то проекция в плоскости xOy (z = 0 ) это будет окружность, каноническое уравнение которой \(x^2+y^2=R^2\). Чтобы составить поверхности, образованной вращением вокруг оси Oz кривой, нужно в уравнении \(z = \frac{4}{x^2}\) заменить \(x^2\) на \(x^2 + y^2\). Итоговое уравнение будет иметь вид $$ z = \frac{4}{x^2} => z = \frac{4}{x^2 + y^2}$$
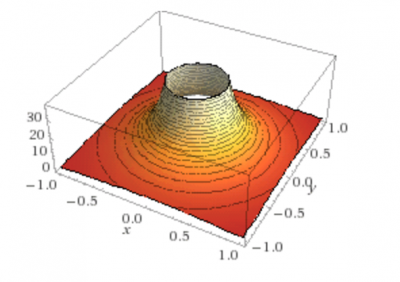
2. Схематический чертеж: