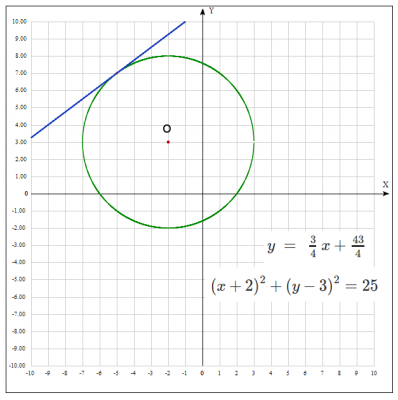
Завдання: Скласти рівняння дотичної до кола з центром (-2;3) і радіусом 5 в точці (-5;7)
Рішення: рівняння дотичної в точці дорівнює $$ y = f (x_0) + f '(x_0) (x-x_0) \quad (1) $$
Канонічні рівняння кола $$ (x - a) ^ 2 + (y - b) ^ 2 = R ^ 2 $$ де (a; b) - центр кола. Підставляємо координати і значення радіусу, отримуємо $$ (x + 2) ^ 2 + (y-3) ^ 2 = 25 $$
Знайдемо похідну функції окружності $$ ((x + 2) ^ 2 + (y-3) ^ 2) '= (25)' = > 2 (x + 2) + 2 (y-3) y '= 0 = > $$$$ y' = - \frac{x + 2}{y-3} $$
Рівняння дотичних в точці з координатами (- 5; 7)
Знайдемо значення похідної функції в точці \(x_0 = -5; y_0 = 7 \), отримуємо \(f '(- 5 ) = - \frac{x + 2}{y-3} = - \frac{- 5 + 2}{7-3} = \frac{3}{4} \)
Підставляємо отримані значення в рівняння дотичної в точці (1) $$ y = 7 + \frac{3}{4} (x + 5) = \frac{3 }{4} x + \frac{43}{4} $$
Відповідь: рівняння дотичної до кола \((x + 2) ^ 2 + (y-3) ^ 2 = 25 \) в точці (-5; 7) дорівнює: \(y = \frac{3}{4} x + \frac{43}{4} \)