Записати канонічне рівняння кривої \( 9x^2+25y^2-36x+50y-139=0 \).
Знайти координати її фокусів та ексцентриситет
1. Запишемо рівняння кривої в канонічному вигляді.
В даному рівнянні є тільки члени другого і першого ступеня (немає змішаного твори), тому канонічне рівняння будемо отримувати методом виділення повного квадрата.
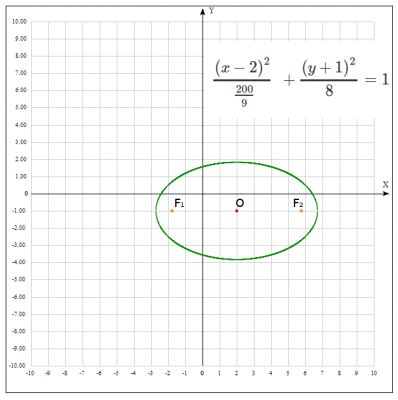
$$ 9x^2+25y^2-36x+50y-139 = 0 = > $$$$ 9(x^2-4x)+25(y^2+2y)-139=0 = > $$ доповнюємо члени в дужках до повного квадрата $$ 9(x^2-2*2x + 4 - 4)+25(y^2+2*1*y+1-1)-139 = 0 => $$$$ 9(x - 2)^2 - 36+25(y+1)^2-25-139 = 0 = > $$$$ 9(x - 2)^2 +25(y+1)^2 - 200 = 0$$ Отримали рівняння еліпса. Як відомо канонічне рівняння еліпса $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ розділимо рівняння на 200 $$ \frac{(x - 2)^2}{\frac{200}{9}} + \frac{(y + 1)^2}{8} = 1 => \quad (1) $$
Отримали рівняння еліпса.
2. Знайти координати фокусів, центру.
Розглянемо отримане рівняння еліпса \( \frac{(x - 2)^2}{\frac{200}{9}} + \frac{(y + 1)^2}{8} = 1 \) з рівняння видно, що координата центру еліпса \(O (2; -1)\) .
Також з рівняння визначимо півосі еліпса \(a = \frac{10\sqrt{2}}{3} \approx 4.71 \) і \(b = 2\sqrt{2} \approx 2.83 \).
Знайдемо координати фокусів. Визначимо, на якій осі лежить фокальна вісь \(F_1F_2 \). Т.я. \( a > b \), то фокальна вісь лежить на (уздовж) осі Ox, тому координати фокусів будуть наступними: \(F_1(-c+x_0; 0 +y_0) \) і \(F_2 (c+x_0; 0+y_0) \), де \(c = \sqrt{a ^ 2-b ^ 2} => \) $$c = \sqrt{\frac{200}{9} - 8 } = \frac{8\sqrt{2}}{3} \approx 3.77 $$ де \((x_0;y_0)\) - координати центру еліпса \(O (-1; -4)\).
Координати фокусів будуть наступні \( F_1 (- 3.77 + 2; 0 - 1) \) і \(F_2 ( 3.77 +2; 0 - 1) \) => \( F_1 (- 1.77 ; - 1) \) і \(F_2 ( 5.77; - 1) \).
3. Знайти ексцентриситет еліпса.
Ексцентриситет еліпса розраховується за формулою \( \epsilon = \frac{c}{a} \) => \( \epsilon = \frac{2\sqrt{7}}{8} = \frac{\frac{8\sqrt{2}}{3}}{ \frac{10\sqrt{2}}{3}} =\frac{4}{5} = 0.8\)
4. Будуємо малюнок: