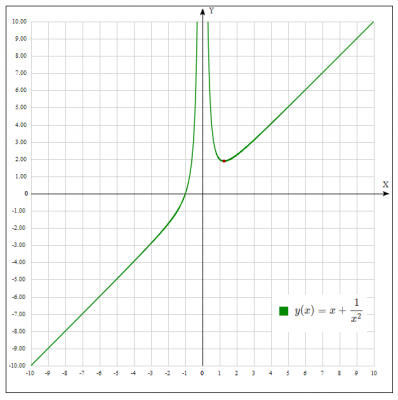
Знайдемо найбільше і найменше значення функції \( y = x + \frac {1} {x ^ 2} \) на відрізку \(x \in (0; 4] \).
Найбільшим, найменшим значенням функції на відрізку можуть бути точки:
1. максимуму,
2. мінімуму,
3. або значення функції на кінцях відрізка.
Алгоритм знаходження найбільшого і найменшого значення функції на відрізку:
1. Область визначення .
Перевіряємо, чи є інтервал \(x \in (0; 4] \) підмножиною області визначення функції.
Є. Область визначення \( x \ne 0; \quad x \in (- \infty; 0) \cup (0; + \infty) \)
2. Знаходимо стаціонарні точки:
Для знаходження стаціонарних точок знайдемо першу похідну і прирівняємо її у нулю $$ y '= ( x + \frac {1} {x ^ 2})' = 1 - \frac {2} {x ^ 3} $$ прирівняємо похідну до нуля $$ y '= 1 - \frac {2} {x ^ 3} = 0 = gt; x ^ 3-2 = 0; \quad x = \sqrt [ 3] {2} $$ функція має одну стаціонарну точки.
3 Вибираємо з отриманих стаціонарних точок ті, які належать заданому відрізку.
Функція \(y \) відрізку (0; 4] має точку ймовірного екстремуму (мінімуму, максимуму ) \(x = \sqrt [3] {2} \approx 1.26 \). Точка потрапляє в заданий відрізок.
4. Знаходимо значення функції в стаціонарних точках (див п.2).
Знайдемо значення функції в цій точці
$$ f (\sqrt [3] {2}) = x + \frac {1} {x ^ 2 } \approx 1.89 $$
5. знаходимо значення функції на кінцях заданого відрізка:
Для лівої граничної точки відрізка знаходимо межу $$ \lim_ {x \to 0 + 0 } f (0) = \lim_ {x \to 0 + 0} (x + \frac {1} {x ^ 2}) = + \infty $$
Для правої граничної точки відрізка знаходимо значення функції в точці $$ f (4) = x + \frac {1} {x ^ 2} \approx 4.06 $$
6. З отриманих значень функції (п.3 і п.4) вибираємо найбільше і найменше значення.
Порівнюємо результати, отримані в п.3 і п.4
Найбільше значення вибираємо з точок максимуму (якщо є) і значень функції на кінцях відрізка.
Найменше значення вибираємо з точок мінімуму (якщо є) і значень функції на кінцях відрізка.
Про найбільше значення функції на відрізку сказати нічого не можна, тому що межа функції в лівої граничної точці відрізка \( \infty \)
Найменше значення функції на відрізку - значення функції в точці мінімуму \(min_{x \in (0; 4]}f(x) = f(\sqrt [3] {2}) = 1.89 \)
Перевіряємо отриманий результат, будуємо графік функції: