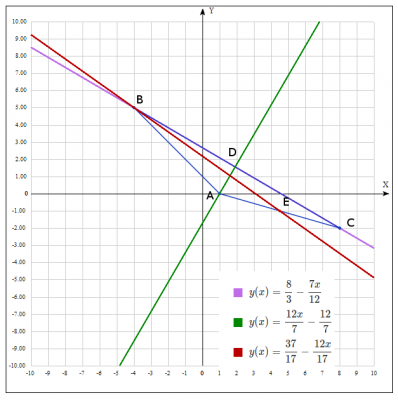
Дано координати вершин трикутника АВС: А(1 ; 0), В(-4 ; 5 ), С(8 ; -2)
Знайти:
1) довжину ВС
2) рівняння висоти АD на сторону ВС
3) рівняння медіани ВЕ
4) точку перетину медіани ВЕ та висоти АD
5) довжину висоти АD
6) кут між прямими АD і ВЕ
Розв'язання:
1) Довжина BC
Знайдемо довжину сторони \(BC \), для цього скористаємося формулою відстані між двома точками \(d = \sqrt{(x_2-x_1) ^ 2 + (y_2-y_1) ^ 2} \quad (1) \), підставляємо координати точок В (-4 ; 5 ), С (8 ; -2), отримуємо: $$ d_{BC} = \sqrt{(8 + 4) ^ 2 + (- 2- 5) ^ 2} \approx 13,89 $$
Відповідь: довжина сторони \(BC \): \(d_{BC} \approx 13,89 \)
2) Рівняння висоти АD на сторону ВС
План знаходження рівняння висоти AD наступний:
1. Знайдемо рівняння сторони \(BC \) за формулою рівняння прямої, що проходить через дві задані точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (2.1) \)
Підставляємо координати вершин: В(-4 ; 5 ), С(8 ; -2) в рівняння (2.1) $$ \frac{x+4}{8+4} = \frac{y-5}{-2-5} => y = \frac{8}{3}- \frac{7}{12}x$$ Отримали рівняння прямої \(BC \) $$ y = \frac{8}{3}- \frac{7}{12}x $$
Висота \(AD\) опущена з вершини \(A\)на сторону \(BC \), тобто з умови відома одна координата точки А(1 ; 0) і напрям - пряма перпендикулярна прямий \(BC \).
Скористаємося властивістю кутових коефіцієнтів перпендикулярних прямих: \(k_1 = - \frac{1}{k_2} \quad (2.2) \).
Знайдемо кутовий коефіцієнт висоти \(AD\) з рівняння (2.1)
Отримали \(k_{BC} = - \frac{7}{12} => \) \(k_{AD} = - \frac{1}{BC} = \frac{12}{7} \).
Знайдемо рівняння висоти \(AD\), для цього скористаємося рівнянням прямої що проходить через задану точку А(1 ; 0) в заданому напрямку \(k_{AD} = \frac{12}{7} \) $$ y - y_0 = k (x - x_0) \quad (2.3) $$ отримаємо $$ y - 0 = \frac{12}{7} (x - 1) => y = \frac{12}{7}x - \frac{12}{7}$$
Відповідь: рівняння висоти AD: \( y = \frac{12}{7}x - \frac{12}{7}\)
3) Рівняння медіани BE
Для знаходження медіани BE є координата однієї точки В(-4 ; 5 ), а координати другої точки прямий E знайдемо як координати середини відрізка \(AC \), де А(1 ; 0), С(8 ; -2) за формулою \(E(\frac{x_A + x_C}{2}; \frac{y_A + y_C}{2}) \) => \(E(\frac{1 + 8}{2}; \frac{0-2}{2}) \) => \(E(4,5; -1) \)
Знаходимо рівняння прямої \(BE \) за формулою рівняння прямої, що проходить через дві задані точки \(В(-4 ; 5 )\) і \(E(4,5; -1)\) рівняння (1) $$ \frac{x+ 4}{4,5 +4} = \frac{y-5}{-1 -5} => y = \frac{37}{17}- \frac{12}{17}x $$
Відповідь: рівняння медіани BE: \( y = \frac{37}{17}- \frac{12}{17}x\)
4) Точку перетину медіани ВЕ та висоти АD
Для знаходження точки перетину знайдемо рішення системи рівнянь. Складемо систему рівнянь з рівнянь медіани \(BE\): \( y = \frac{37}{17}- \frac{12}{17}x\) і висоти \(AD\): \( y = \frac{12}{7}x - \frac{12}{7}\) $$\begin{cases} y = \frac{37}{17}- \frac{12}{17}x\\ y = \frac{12}{7}x - \frac{12}{7} \end{cases} =>\begin{cases}17 y = 37- 12x\\ 7y =12x - 12\end{cases} => $$$$ \begin{cases} 24y = 25\\ 7y =12x - 12\end{cases} =>\begin{cases} y = \frac{25}{24} \\ x \approx 1.61 \end{cases}$$
Відповідь: точку перетину медіани ВЕ та висоти АD має координати \((1.61;1.04)\)
5) Довжину висоти АD
Довжину висоти AD будемо шукати як відстань від точки А(1 ; 0) до прямої BC за формулою $$ d = \frac{| Ax_0 + By_0 + C |}{\sqrt{A^2 + B^2}} \quad(5) $$ де \((x_0; y_0) \) - координати точки С(1;2), а
\(Ax_0 + By_0 + C = 0 \) - загальне рівняння прямої, відстань до якої шукається. У нашому випадку це рівняння сторони BC
$$y = \frac{8}{3}- \frac{7}{12}x => 7x +12y - 32 =0 => A = 7; \quad B = 12 $$ Підставляємо дані у формулу $$ d_{AD} = \frac{| 7*1 +12*0 - 32 |}{\sqrt{7^2 + 12^2}} \approx 1.8 $$
Відповідь: довжина висоти AD: \(d_{AD} \approx 1.8 \)
6) Кут між прямими АD і ВЕ
Кут між прямими AD і BE - \( \beta \) будемо шукати за формулою $$ tg \beta = | \frac{k_2-k_1}{1 + k_1k_2} | \quad (6) $$
\(k_1, k_2 \) - кутові коефіцієнти прямих AD і BE.
Кутовий коефіцієнт прямої AD дорівнює \(k_ {AD} = \frac{12}{7} \).
Кутовий коефіцієнт прямої BE дорівнює \(k_ {BE} = - \frac{12}{17} \).
Підставляємо кутові коефіцієнти (6) $$ tg \beta = | \frac{ \frac{12}{17}-\frac{12}{7} }{1 +\frac{12}{17}(-\frac{12}{7})} | = \frac{24}{5} => \beta \approx 78^0 $$
Відповідь: кут між прямими АD і ВЕ дорівнює: \( \quad \beta \approx 78^0 \)