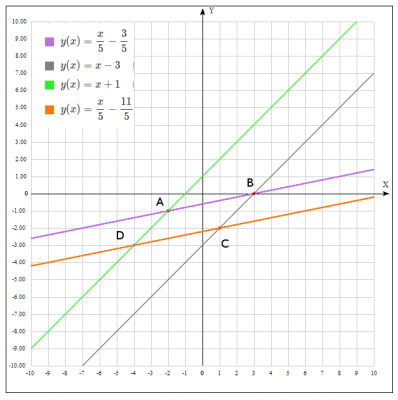
Дано: параллелограмм ABCD и координаты вершин A(-2;-1), B(3;0), C(1;-2)
Найти: координаты вершины D
Решение: Параллелограмм - это четырехугольник у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Отсюда получаем алгоритм решения задачи
1. Находим уравнения двух сторон по известным координатам вершин.
2. Находим уравнения параллельных сторон по известной координате одой из вершин и воспользовавшись условием параллельности сторон.
3. Находим координаты точки пересечения, полученных сторон.
Алгоритм решения:
1. Находим уравнения сторон AB и BC.
Из условия задачи известны координаты вершин A(-2;-1), B(3;0), C(1;-2), поэтому уравнения сторон будем находить по формуле уравнения прямой, проходящей через две заданные точки $$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1)$$
Уравнение стороны AB при известных координатах вершин A(-2;-1), B(3;0). Подставляем координаты в уравнение (1), получаем $$ \frac{x+2}{3+2} = \frac{y+1}{0+1} => y = \frac{1}{5}x - \frac{3}{5}$$
Уравнение стороны BC при известных координатах вершин B(3;0), C(1;-2). Подставляем координаты в уравнение (1), получаем $$ \frac{x-3}{1-3} = \frac{y-0}{-2-0} => y = x - 3$$
2. Находим уравнения параллельных сторон параллелограмма.
Через вершины параллелограмма проходят прямые \(AD||BC\) и \(CD||AB\). О прямых AD и CD известно, что они проходят через вершины с известными координатами и параллельны известным прямым. Воспользуемся свойством параллельных прямых: угловые коэффициенты параллельных прямых равны \(k_1=k_2\).
Найдем уравнение прямой \(AD\).
Для этой прямой известна координата A(-2;-1) и угловой коэффициент, который равен угловому коэффициенту прямой \(k_{BC} = 1 => k_{AD} = 1\).
Воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении $$ y - y_0 = k(x-x_0) \quad (2)$$ Подставляем данные A(-2;-1) и \(k_{AD} = 1\), получаем $$ y +1 = 1(x+2) => y = x+1 $$
Найдем уравнение прямой \(CD\).
Для этой прямой известна координата C(1;-2) и угловой коэффициент, который равен угловому коэффициенту прямой \(k_{AB} = \frac{1}{5} => k_{CD} = \frac{1}{5}\).
Воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении $$ y - y_0 = k(x-x_0) $$ Подставляем данные C(1;-2) и \(k_{CD} = \frac{1}{5}\), получаем $$ y +2 = \frac{1}{5}(x-1) => y = \frac{1}{5}x-\frac{11}{5} $$
3. Находим координаты точки пересечения, полученных сторон\(AD\) и \(CD\).
Решим систему уравнений $$ \begin{cases} y = x+ 1 \\ y = \frac{1}{5}x-\frac{11}{5} \end{cases} => $$$$ \begin{cases} 0 = \frac{4}{5}x+\frac{16}{5} \\ y = \frac{1}{5}x-\frac{11}{5} \end{cases} => \begin{cases} x = -4 \\ y = -3 \end{cases} $$ Подучили координаты точки \(D(-4; -3) \)
Ответ: координаты искомой вершины параллелограмма \(D(-4; -3) \).