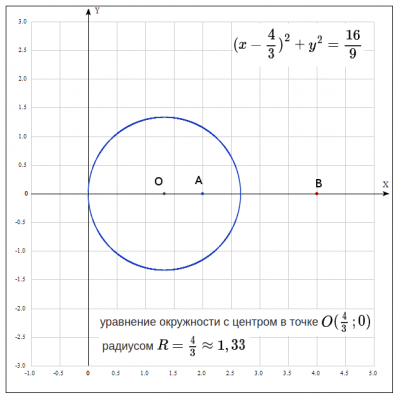
Написать уравнение кривой, каждая точка которой вдвое ближе к точке А (2:0), чем к точке В (4:0).Сделать чертеж.
Решение: составим уравнение линии, расстояние от каждой точки которой до точки А(2;0) в два раза ближе, чем к точке В (4:0).
Пусть B(x;y) - точка, которая принадлежит искомой кривой, найдем расстояние от этой точки
до точки А(2;0): в декартовой системе координат расстояние между точками рассчитывается по формуле $$d = \sqrt{(x_2−x_1)^2+(y_2−y_1)^2} \quad (1)$$ подставляем координаты и получаем $$d_1 = \sqrt{(x−2)^2+(y−0)^2}$$
до точки B(4;0) подставляем координаты и получаем $$d_2 = \sqrt{(x−4)^2+(y−0)^2}$$
Согласно условия задачи, расстояние до точки А(2;0) - \(d_1\) в два раза меньше, чем до точки B(4;0) \(d_2\), т.е. \( 2d_1 = d_2 \quad (2)\)
Подставляем в (2) уравнения расстояний: $$ 2\sqrt{(x−2)^2+y^2} =\sqrt{(x−4)^2+y^2}=> 4(x−2)^2+4y^2 = (x−4)^2+y^2 =>$$$$ 4x^2 - 16x + 16+4y^2 = x^2 - 8x +16+y^2 => 3x^2 - 8x +3y^2 = 0 => $$ получили уравнение окружности. Приведем его к каноническому виду \((x-a)^2+(y-b)^2=R^2\), где \((a;b)\) - центр окружности. Для этого выделим полный квадрат $$3(x^2 - 2\frac{4}{3}x + \frac{16}{9} -;\frac{16}{9}) +3y^2 = 0 => (x^2 - 2\frac{4}{3}x + \frac{16}{9} -\frac{16}{9}) +y^2 = 0 =>$$$$ (x - \frac{4}{3})^2 -\frac{16}{9}+y^2 = 0 =>(x - \frac{4}{3})^2 +y^2 =\frac{16}{9}$$ Получили уравнение окружности с центром в точке \(O(\frac{4}{3};0)\) и радиусом \(R = \frac{4}{3} \approx 1,33\)
Ответ: получили геометрическое место точки - окружность \( (x - \frac{4}{3})^2 - \frac{16}{9} +y^2 = 0 \)