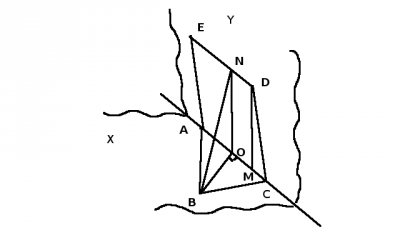
В задаче у нас есть две плоскости, назовем их \(X\) и \(Y\). Нам необходимо найти косинус угла между ними. В плоскости \(X\) лежит треугольник \(ΔABC\), а в плоскости \(Y\) - ромб \(ACDE\). Для начала построим отрезок \(BN\) - перпендикуляр из точки \(B\) к прямой \(DE\). Опустим перпендикуляр из вершины \(B\) на гипотенузу \(AC\) в точку \(O\), а затем из этой точки постоим прямую, перпендикулярную \(AC\). По условию задачи \(ACDE\) - ромб, то эта прямая будет перпендикулярна и стороне \(ED\) и будет пересекать ее в точке \(N\). Проведем плоскость через две прямые \(BO\) и \(ON\). Эта плоскость перпендикулярна прямой \(DE\), т.е. перпендикуляр из точки \(B\) к прямой \(DE\) лежит в этой плоскости. Эти все рассуждения нужны для того, чтобы рассмотреть треугольник \(ΔNBO\) в котором \(\angle NOB\) - искомый, т.е. нужно найти \(\cos \angle NOB\). В этом треугольнике известна \(BN = 4\sqrt{5}\). Нам не известно, является ли это треугольник прямоугольным, поэтому для нахождения косинуса воспользуемся теоремой косинусов. $$с^2 = a^2 + b^2 - 2ab*\cos \alpha => \cos \alpha = \frac{a^2+b^2-c^2 }{2ab}$$Т.о. чтобы решить задачу нам нужно найти еще две стороны треугольника. \(BO\) найдем из треугольника \(ΔABC\). Т.к. это равнобедренный прямоугольный треугольник, то т.О делит гипотенузу \(AC\) пополам. Треугольник \(BOM\) - прямоугольный равнобедренный треугольник \(\angle ACB = 45^0\) по условию, то $$BO =OC = \frac{1}{2}AC = \frac{1}{2}\frac{AB}{\sin{\angle ACB}}=\frac{1}{2}\frac{AB}{\sin{45^0}} =$$$$ = \frac{1}{2}\frac{AB}{\frac{1}{\sqrt 2}} = \frac{1}{2}8\sqrt 2 = 4\sqrt 2$$$$BO = 4\sqrt 2 => AC = 8\sqrt 2$$Найдем \(ON = DM\). Я опустил перпендикуляр из точки \(D\), чтобы рассмотреть \(ΔMDC\) и найти \(DM\). По условию \(AC = DC\) как стороны ромба, а из свойства ромба \(\angle DCM = 180^0 - \angle CAE = 180^0 - 45^0 \). Из этого прямоугольного треугольника получаем $$NO=DM=DC*\sin{\angle DCM} = 8\sqrt 2*\sin{(180^0 - 45^0)} = 8\sqrt 2*\sin{45^0} = 8\sqrt 2*\frac{1}{\sqrt 2} = 8$$Подставляем полученные данные в формулу косинусов, где \(c = BN = 4\sqrt 5;\quad a = BO =4\sqrt 2; \quad b = NO = 8 \)$$ \cos \angle NOB = \frac{(4\sqrt 2)^2+8^2-(4\sqrt 5)^2 }{2*4\sqrt 2 *8} = \frac{1}{4\sqrt 2}$$



