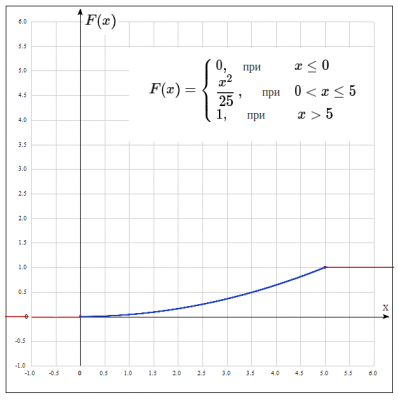
Дано: Случайная величина задана интегральной функцией распределения. $$ F(x) = \begin{cases} 0, \quad при & x \leq 0\\ \frac{x^2}{25}, \quad при & 0 < x \leq 5 \\ 1, \quad при & x > 5 \end{cases} $$
Найти:
1) дифференциальную функцию f(x) (плотность распределения вероятности)
2) математическое ожидание и дисперсию
3) построить графики F(x),f(x)
Решение:
1. Найдем плотность распределения (дифференциальную функцию f(x)).
плотность распределения и функция распределения случайной величины связаны соотношением $$F'(x) = f(x)$$ найдем плотность распределения на каждом интервале:
\((-\infty;0]\) плотность равна \(f(x) = F'(x) = (0)' = 0\)
\((0;5]\) плотность равна \(f(x) = F'(x) = (\frac{x^2}{25})' = \frac{2}{25}x\)
\((5;+\infty)\) плотность равна \(f(x) = F'(x) = (1)' = 0\)
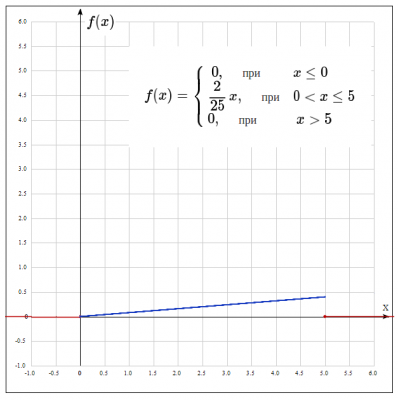
Получили следующую функцию плотности распределения $$ f(x) = \begin{cases} 0, \quad при & x \leq 0 \\ \frac{2}{25}x, \quad при & 0 < x \leq 5 \\ 0, \quad при & x > 5 \end{cases}$$
2. Найдем математическое ожидание.
Математическое ожидание случайной величины X будем искать по формуле $$M(X) = \int_a^bxf(x)dx$$ С учетом трех интервалов получаем $$M(X) = \int_{-\infty}^0x*0dx+\int_0^{5}x^2\frac{2}{25}dx+\int_5^{\infty}x*0dx = \frac{2}{75}x^3|_0^5 = \frac{10}{3} $$
Найдем дисперсию случайной величины.
Дисперсия случайной величины \(X\), все значения которой принадлежат отрезку \([a,b]\) определяется формулой $$D(X) = \int_a^b(x-M(x))^2f(x)dx = \int_a^bx^2f(x)dx - (M(X))^2$$ С учетом трех интервалов получаем $$D(X) = \int_{-\infty}^{\infty}x^2f(x)dx - (\frac{10}{3})^2 = $$$$ = \int_{-\infty}^{0}x^2*0dx + \int_{0}^{5}x^3*\frac{2}{25}dx + \int_{5}^{\infty}x^2*0dx - (\frac{10}{3})^2 = $$$$ = \frac{x^4}{50}|_0^5 - (\frac{10}{3})^2 = \frac{25}{2} - (\frac{10}{3})^2 \approx 1.39$$
3. Построим графики F(x),f(x)