Решение: нам нужно разместить вершины треугольника в вершинах 8-угольника. Очень важно - то, что стороны фигур не совпадают. Т.е. вершины треугольника не должны лежать на одной стороне восьмиугольника.
Решать задачу будем путем размещением последовательно вершин и проводить расчет количества этих размещений.
1. размещаем первую вершину \(A\).
Первую вершину можно разместить \( n_A = 8\) способами (во всех вершинах \(1,2,3,4,5,6,7,8\)).
Для дальнейшего анализа рассмотрим случай - вершина \(A\) находится в вершине с номером \(1\)
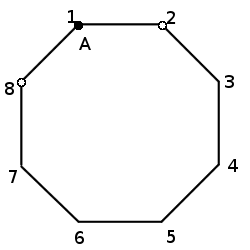
2. размещаем вторую вершину \(B\).
Осталось 7 свободных мест.
Учтем условие задачи: вершины треугольника не должны лежать на одной стороне восьмиугольника, т.е. вершины справа и слева от вершины \(A\), т.е. вершины с номерами \(2\) и \(8\) - всегда свободны. Назовем их "пустыми вершинами при вершине \(A\)". Осталось свободных 5 вершин с номерами \(3,4,5,6,7\).
Вторую вершину можно разместить \( n_B = 5\) способами.
3. размещаем третью вершину \(C\).
Рассмотрим размещение вершины \(B\) подробнее и определим соответствующее количество способов размещения точки \(C\):
Пусть вершина \(B\) находится в точке с номером \(3,7\). Эти вершины характерны тем, что с одной стороны у них есть "пустая вершина при вершине \(A\)", а с другой стороны "пустая вершина при вершине \(B\)". В этом случае третью вершину \(C\) можно разместить в 5-2 =3 вершинах.
Для этих двух точек применим правило произведения:
Правило произведения: Если объект \(A\) можно выбрать из множества объектов \(m\) способами и после каждого такого выбора объект \(B\) можно выбрать \(n\) способами, то пара объектов (A,B) в указанном порядке может быть выбрана \(m*n\) способами.
В первом случае у нас есть 2 вершины, в которых размещаем \(B\), т.е. m = 2 и 3 вершины, где размещаем \(C\) n=3. В этом случае количество размещений на восьмиугольнике пар вершин \(BC\) будет равна \(n_{BC1} = m*n = 2*3 =6\).
Пусть вершина \(B\) находится в точке с номером \(4,5,6\). Эти вершины с обеих сторон должны иметь "пустые вершины при вершине \(B\)". В этом случае третью вершину можно разместить в 5-3 =2 вершинах, т.е \(n_{C2}=2\)
Для этих двух точек применим правило произведения, получаем у нас есть 3 вершины, в которых размещаем \(B\), т.е. m = 3 и 2 вершины, где размещаем \(C\) n=2. В этом случае количество размещений на восьмиугольнике пар вершин \(BC\) будет равна \(n_{BC2} = m*n = 3*2 =6\).
Проверяем: количество размещений вершины \(B\) в двух рассматриваемых случаях \(n_B = 2 + 3 = 5 \), что соответствует п.2
Для двух этих случаев \(n_{BC1} = 6\), \(n_{BC2} = 6\) применим правило суммы:
Правило суммы: если объект \(А\) можно выбрать из множества объектов \(m\) способами, а другой объект \(В\) может быть выбран \(n\) способами, то выбрать либо объект \(А\) либо \(В\) можно \(m+n\) способами.
Получаем \(n_{BC} = n_{BC1}+ n_{BC2} = 6 + 6 = 12\)
Получили, что при фиксированном размещении вершины \(A\) количество размещений вершин \(n_{BC} = 12 = m\). Вершину \(A\) мы можем разместить на восьмиугольнике \( n_A = n = 8 \)
Для этих двух выборок применим правило произведения и получим количество искомых треугольников: $$N = m*n = 12*8 = 96$$
Ответ: существует \(n=96\) треугольников, вершины которых являются вершинами данного выпуклого 8-угольника, а стороны не совпадают со сторонами этого многоугольника.



