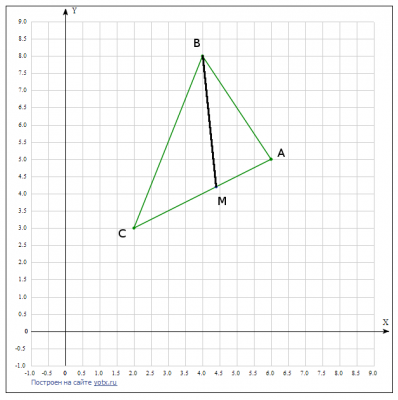
Дано треугольник ABC. A(6;5),B (4;8),C (2;3).
Найти длину биссектрисы BM.
Решение: для нахождения длины биссектрисы найдем точку пересечения биссектрисы \(BM\) и стороны \(AC\), пусть это будет точка \(M\), т.е. найдем координаты этой точки. Зная координаты двух точек \(B\) и \(M\) найдем длину искомого отрезка \(BM\) по формуле $$BM = \sqrt{(x_M-x_B)^2+(y_M-y_B)^2}$$
1. Найдем координаты точки \(M\) - точки пересечения биссектрисы \(BM\) и стороны \(AC\).
Для нахождения точки пересечения \(M\) воспользуемся:
свойством биссектрисы угла треугольника: биссектриса внутреннего угла треугольника делит противоположную углу сторону на отрезки, пропорциональные двум другим сторонам \(\frac{CM}{MA}=\frac{CB}{AB} = \lambda\), т.е. таким образом мы найдем коэффициент \(\lambda\), затем воспользуемся формулой координаты точки, которая делит отрезок \(BC\) в заданном отношении \(\lambda\) и найдем координаты точки \(M\).
1.1 Найдем длины отрезков \(AB\), \(CB\).
Из условия задачи известны координаты точек \(A(6;5),B (4;8),C (2;3)\).
$$AB = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2}= \sqrt{(4-6)^2+(8-5)^2} =\sqrt{2^2+3^2}=\sqrt{13}$$
$$CB = \sqrt{(x_B-x_C)^2+(y_B-y_C)^2}= \sqrt{(4-2)^2+(8-3)^2} =\sqrt{2^2+5^2}=\sqrt{29}$$
1.2. Найдем коэффициент \(\lambda\)
$$ \lambda =\frac{CM}{MA}=\frac{CB}{AB}= \sqrt{\frac{29}{13}}$$
1.3.Найдем координаты точки \(M\)
при известных координатах концов отрезка \(CA\) точек \(C (2;3); A(6;5)\)
Воспользуемся формулой координаты точки, которая делит отрезок в заданном отношении \(\lambda\)
$$x = \frac{x_1+\lambda x_2}{1+\lambda}$$
Подставляем координаты концов отрезка, учтем, что в формуле, получаем
$$x_M=\frac{2+6\sqrt{\frac{29}{13}}}{1+\sqrt{\frac{29}{13}}} \approx 4.4 $$
$$y_M = \frac{3+5\sqrt{\frac{29}{13}}}{1+\sqrt{\frac{29}{13}}} = \approx 4.2$$
Получили координаты точки \(M(4.4;4.2)\)
2. Найдем длину искомого отрезка \(BM\)
при известных координатах точек \(B (4;8)\), \(M(4.4;4.2)\) по формуле \(BM = \sqrt{(x_M-x_B)^2+(y_M-y_B)^2} \) получаем $$BM = \sqrt{(4.4-4)^2+(4.2-8)^2} \approx 3.82$$
Ответ: длина биссектрисы \(BM \approx 3.82\).