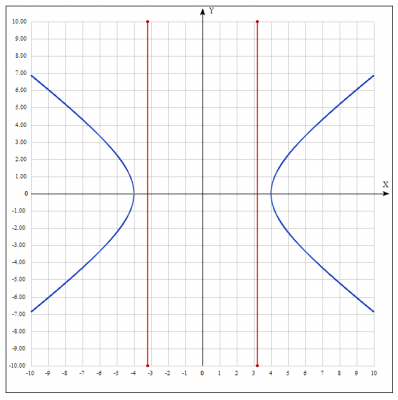
Дано: Составить уравнение гиперболы, симметричной относительно координатных осей, с фокусами на оси ОХ, если расстояние между директрисами равно \(\frac{32}{5}\), а мнимая ось равна 6
Решение:
Согласно условия задачи, фокусы лежат на оси Ox, т.е. эта ось является действительной.
каноническое уравнение гиперболы с действительной осью Ox, симметричной относительно осей имеет вид $$ \frac{x^2}{a^2} - \frac{y^2}{b^2}=1 \quad (1)$$
Найдем действительную полуось \(a\) и мнимую полуось \(b\)
Согласно условия задачи мнимая ось равна \(2b=6 => b=3\) .
Определение. Директрисами гиперболы называются две прямые, уравнения которых в канонической для гиперболы системе координат имеют вид $$x = \pm \frac{a}{ \epsilon}$$
Обозначение. Расстояние между директрисами обозначается 2d и равно $$ 2d = \frac{2a}{ \epsilon} \quad (2)$$
где \(\epsilon\) - эксцентриситет, который равен $$ \epsilon = \frac{c}{a} = \frac{ \sqrt{a^2+b^2}}{a} \quad (3)$$
Подставляем (3) в (2) $$ 2d = \frac{2a}{ \frac{ \sqrt{a^2+b^2}}{a} } = \frac{2a^2}{ \sqrt{a^2+b^2}}$$
Из полученной формулы выразим значение \(a\) - действительная полуось $$ 2d = \frac{2a^2}{ \sqrt{a^2+b^2}} => $$
Подставляем данные из условия задачи:
\(2d = \frac{32}{5}\)
\(b = 3\), получаем $$ \frac{32}{5} = \frac{2a^2}{ \sqrt{a^2+9}} => 16\sqrt{a^2+9} = 5a^2 => $$$$ 16^2(a^2+9) = 5^2a^4 => 5^2a^4 - 16^2a^2-16^2*9 =0$$ Найдем корни уравнения четвертой степени $$ a^2_{1,2} = \frac{16^2 \pm \sqrt{16^4+4*5^2*16^2*9}}{2*5^2} => $$$$ a_1^2=16 \quad a_2^2 = -\frac{144}{25} $$
Выбираем положительный ответ $$a^2 = 16 => a = 4$$
Подставляем полученный результаты в (1) и получаем уравнение гиперболы $$ \frac{x^2}{4^2} - \frac{y^2}{3^2}=1 $$
Ответ: уравнение гиперболы \( \frac{x^2}{16} - \frac{y^2}{9}=1 \)