Правильное решение геометрической задачи зависит от правильно построенного рисунка. Рассмотрим рисунок.
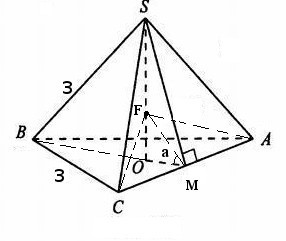
Рассмотрим правильную треугольную пирамиду. \(SO\) - высота пирамиды, \(O\) - центр правильного (равностороннего) треугольника в основании, т.е. расстояние от любой точки высоты до вершин основания одинаковые, т.е. \(FA=FB=FC\). Нас интересуют \(FA=FC\) для построения искомого угла и его анализа. Построим искомый угол. Точки \(F\) и \(A\) принадлежат плоскости \(MFC\), соединим их и рассмотрим треугольник \(ΔCFA\). Это равнобедренный треугольник, т.к. \(FA=FC\). Высота из вершины \(F\) этого треугольника является также его медианой (свойство равнобедренных треугольников), т.е. высотой будет \(FM\). Теперь в треугольнике \(ΔABC\) опустим высоту в точку \(M\), это будет \(BM\), т.к. из свойства медиан и высот равностороннего треугольника известно, что они совпадают, а точка \(M\) - середина \(AC\) по условию задачи. Получили искомый угол \(\angle{FMO} = \alpha\). Будем искать этот угол из прямоугольного треугольника \(ΔFMO\) $$\mbox{tg}\alpha = \frac{FO}{OM}$$\(OM\) найдем из треугольника \(ΔABC\). Как известно медианы в точке пересечения делятся в пропорции 2:1, начиная от вершины, т.е \(OM = \frac{1}{3}BM\), а \(BM = BC*\sin{60^0} = 3*\frac{\sqrt 3}{2} => OM = \frac{1}{3}*3*\frac{\sqrt 3}{2} = \frac{\sqrt 3}{2}\). Нам еще понадобится \(BO = \frac{2}{3}BM = \frac{2}{3}*3*\frac{\sqrt 3}{2} = \sqrt 3\). Осталось найти \(FO\) из прямоугольного треугольника \(ΔSOB\) по теореме Пифагора \(SO = \sqrt{BS^2 - BO^2} = \sqrt{3^2 - (\sqrt{3})^2} = \sqrt{9-3} = \sqrt{6}\) => по условию задачи \(FO = \frac{1}{3}SO = \frac{1}{3}\sqrt{6} = \sqrt{\frac{2}{3}}\). Подставляем полученные значения в формулу угла $$\mbox{tg}\alpha = \frac{FO}{OM} = \frac{ \sqrt{\frac{2}{3}}}{\frac{\sqrt 3}{2}} = \frac{2\sqrt{2}}{3} = > \alpha = \mbox{arctg}{\frac{2\sqrt{2}}{3}}$$Ответ: угол межу плоскостями равен \( \alpha = \mbox{arctg}{\frac{2\sqrt{2}}{3}}\)



