Составьте уравнение косательной к графику функции у= (-3х^2)+6x+1 в точке пересеения графика с осью

Вспомним уравнение касательной в точке

$$f(x) = f(x_0) + f'(x_0)(x-x_0)$$ , где $x_0$ - точка касания. По условию задачи точка касания - точка пересечения с осью ординат $Oy$, т.е. это точка с координатой $x_0=0$. Составляем уравнение касательной в этой точке:
1. Находим угловой коэффициент касательной в точке $x_0 = 0$, он равен $f'(x) = ((-3х^2)+6x+1)' = -6x+6 => f'(0) = -6*0+6 = 6$. 
2. Находим значение функции в точке касания $f(x_0) = f(0) = (-3*0^2)+6*0+1 = 1$ 
3. Подставляем результат п.1 и п.2 в уравнение касательной $$f(x) = f(x_0) + f'(x_0)(x-x_0) => f(x) = f(0) + f'(0)(x-0) =>$$ $$f(x) = 1 + 6x$$ Проверим графически наше решение. Построим график функции $y = (-3х^2)+6x+1$ и касательную к нему $y = 1 + 6x$ в точке касания $x_0 = 0$

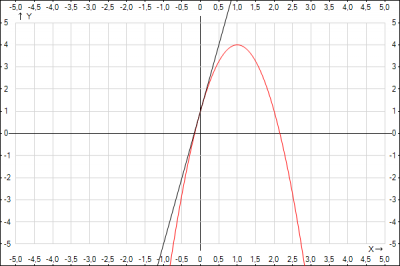
Из графика видно, что решение задачи правильное.

Ответ: уравнение касательной графика функции  $y = (-3х^2)+6x+1$  в точке пересечения графика с осью ординат $y = 1 + 6x$