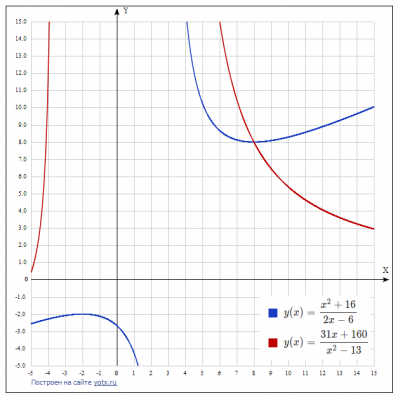
Рішення : дано функції пропозиції \(y = \frac{x^2 + 16}{2x-6} \) та попиту \(y = \frac{31x + 160}{x^2-13} \)
Знайдемо ціле значення ціни одиниці продукції, при якій пропозиція і попит врівноважуються:
Ціна (\(x \)) при якій пропозиція і попит врівноважуються - точка перетину кривих пропозиції та попиту . Для знаходження (\(x \)) ціни одиниці продукції вирішимо рівняння $$ \frac{x^2 + 16}{2x-6} = \frac{31x + 160}{x^2-13} = > $$$$ \begin{cases} (x^2 + 16) * (x^2-13) = (31x + 160) * (2x-6) \\2x-6 \ne 0 \\x^2 13 \ne 0 \end{cases} = > $$
$$ \begin{cases} x^4-59x^2-134x + 752 = 0 \\x \ne 3 \\x \ne \pm \sqrt{13} \end{cases} = > $$ Отримали многочлен четвертого ступеня з цілими коефіцієнтами, згідно умови, цей многочлен має цілий корінь.
Застосуємо теорему : Якщо всі коефіцієнти многочлена: \(f (x) = a_0x_n + a_1x_{n-1} + a_2x_{n-2} + ... + a_{n-2 } x_2 + a_{n-1} x + a_n \) є цілими числами, то всякий цілий корінь цього многочлена є дільником вільного члена \(a_n \)
В отриманому многочлене вільний член \(a_4 = 752 \). Дільниками вільного члена є числа \(\pm 1; \pm 2; \pm 4; \pm 8; \pm 16; \pm 47; \pm 94; \pm 188; \pm 376; \pm 752 \)
Підставляємо почергово числа в многочлен і знаходимо цілий корінь.
Так як ми шукаємо ціну одиниці продукції, то перевіряємо тільки позитивні подільники
\(x = 1: \quad \quad 1^4-59 * 1^2-134 * 1 + 752 = 560 \ne 0 \) - не корінь
\(x = 2: \quad \quad 2^4- 59 * 2^2-134 * 2 + 752 = 264 \ne 0 \) - не корінь
\(x = 4: \quad \quad 4^4-59 * 4^2- 134 * 4 + 752 = -472 \ne 0 \) - не корінь
\(x = 8: \quad \quad 8^4-59 * 8^2-134 * 8 + 752 = 0 \) - корінь
Так як функція четвертого ступеня \(y = x^4-59x^2-134x + 752 \) при x > 8 монотонно зростає, то перевіряти інші дільники немає сенсу (можна в цьому переконатися)
Відповідь : ціле значення ціни одиниці продукції, при якій пропозиція і попит врівноважуються \(x = 8 \)
2. Визначимо еластичність пропозиції та попиту в точці \(x = 8 \)
Еластичність в точці (точкова еластичність) використовується в тому випадку, коли задана функція попиту (пропозиції) і вихідний рівень ціни та величини попиту (або пропозиції). Дана формула характеризує відносну зміну обсягу попиту (або пропозиції) при нескінченно малій зміні ціни (або якого-либо іншого параметра)
Знаходиться еластичність в точці за формулою $$ E = Q '(x) \frac{x}{Q (x)} \quad (1) $$ де
\(Q '(x) \) - похідна від функції пропозиції (попиту)
\(x \) - ринкова ціна
\(Q (x) \) - функція пропозиції (попиту) при ринковій ціні.
Оцінимо еластичність пропозиції при ціні \(x = 8 \)
Знайдемо відсутні параметри формули (1)
\(x = 8 \) - ринкова ціна в заданій точці
\(Q (x) = \frac{x^2 + 16}{2x-6} = > Q (8) = \frac{8^2 + 16}{2 * 8-6} = 8 \) - значення функції пропозиції при заданій ринковій ціні.
\(Q '(x) = (\frac{x^2 + 16}{2x-6}) '= \frac{1}{2} \frac{2x (x-3) - (x^2 + 16)}{(x-3)^2} = \frac{1}{2} \frac{x^2 -6x -16}{(x-3)^2} \) = > \(Q '(8) = \frac{1}{2} \frac{8^2 -6 * 8 -16}{(8-3)^2} = 0 \) - значення функції пропозиції при заданій ринковій ціні.
Підставляємо у формулу (1) $$ E_{пропоз} (8) = Q '(8) \frac{8}{Q (8)} = 0 \frac{8}{8} = 0 $$
Відповідь : Економічний сенс отриманого значення полягає в тому, що зміна ціни на 1% щодо початкової ціни x = 8 призведе до зміни величини пропозиції на 0%. Отримали \(E = 0 \), або абсолютна нееластичність, коли зміна якого-либо параметра ринкової кон'юнктури не впливає на величину розглянутого фактора (зміна ціни не впливає на пропозицію, графік кривої в околиці цієї точки паралельний осі ціни - x).
Оцінимо еластичність попиту при ціні \(x = 8 \)
Знайдемо відсутні параметри формули (1)
\(x = 8 \) - ринкова ціна в заданій точці
\(Q (x) = \frac{31x + 160}{x^2-13} = > Q (8) = \frac{31x + 160}{x^2-13} = 8 \) - значення функції попиту при заданій ринковій ціні.
\(Q '(x) = (\frac{31x + 160}{x^2 -13}) ' = \frac{31 (x^2-13) - 2x (31x + 160)}{(x^2-13)^2} = - \frac{31x^2 + 320x + 403}{(x^2-13)^2} \) = > \(Q '(8) = - \frac{31 * 8^2 + 320 * 8 + 403}{(8^2-13)^2} \approx -1,9 \) - значення функції попиту при заданій ринковій ціні.
Підставляємо у формулу (1) $$ E_{попит} (8) = Q '(8) \frac{8}{Q (8)} = (-1,9) \frac{8}{ 8} = -1.9 $$
Відповідь : Економічний сенс отриманого значення полягає в тому, що зміна ціни на 1% щодо початкової ціни x = 8 призведе до зміни величини попиту на -1.9%. \(| E | > 1 \), або еластичний попит, коли параметр зростає більш високими темпами, ніж змінюється інший чинник.
Графіки функцій пропозиції та попиту