Рішення : потрібно знайти рівняння прямої, яка проходить через задану точку в заданому напрямку. Скористаємося рівнянням прямої, що проходить через задану точку в заданому напрямку$$ y - y_0 = k (x-x_0) \quad (1) $$
Згідно умови задачі, відомі координати точки, через яку проходить пряма M (1; -4) і напрям - кутовий коефіцієнт шуканої прямий прямий, про яку відомо, що вона утворює кут з відомою прямий \(2x-5y + 1 = 0 => k = \frac{2}{5} \).
Знайдемо кутовий коефіцієнт, використовуємо формулу кута між двома прямими $$ tg (\alpha) = | \frac{k_2-k_1}{1 + k_1k_2} | \quad (2) $$
Згідно умови задачі відомо:
1. кутовий коефіцієнт заданої прямої \(k_1 = \frac{2}{5} \)
2. кут між прямими \(\alpha = 45^0 => tg (\alpha) = tg (45^0) = 1 \)
Підставляємо у формулу (2) і знаходимо невідомий кутовий коефіцієнт $$ | \frac{k_2- \frac{2}{5}}{1+ \frac{2}{5} k_2} | = 1 => | \frac{5k_2- 2}{5+ 2k_2} | = 1 => $$ розкриємо модуль, отримаємо систему рівнянь $$ \begin{cases} \frac{5k_2- 2}{5+ 2k_2} = 1 & при & \frac{5k_2- 2}{5+ 2k_2}> 0 \\\frac{5k_2- 2}{5+ 2k_2} = -1 & при & \frac{5k_2- 2}{5+ 2k_2} < 0 \end{cases} => $$$$ \begin{cases} 5k_2- 2 = 5+ 2k_2 & при & (5k_2- 2) (5+ 2k_2)> 0 \\5k_2- 2 = -5- 2k_2 & при & (5k_2- 2) (5+ 2k_2) < 0 \\k_2 \ne - \frac{5}{2} \end{cases} => $$$$ \begin{cases} k_2 = \frac{7}{3} & при & (k_2- \frac{2}{5}) (k_2 + \frac{5}{2})> 0 \\k_2 = - \frac{3}{7} & при & (k_2- \frac{2}{5}) (k_2 + \frac{5}{2}) < 0 \\k_2 \ne - \frac{5}{2} \end{cases} => \begin{cases} k_2 = \frac{7}{3} \\k_2 = - \frac{3}{7} \end{cases} $$
підставляємо отримані кутові коефіцієнти в рівняння прямої (1), отримуємо два рівняння шуканої прямої:
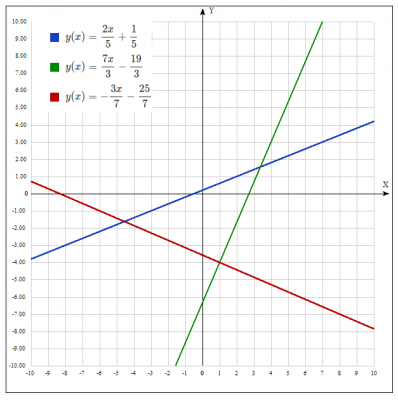
1. \( y + 4 = \frac{7}{3} (x-1) => y = \frac{7}{3} x - \frac{19}{3} \)
2. \( y + 4 = - \frac{3}{7} (x-1) => y = - \frac{3}{7} x - \frac{25}{7} \)
Дві отримані прямі перпендикулярні між собою, так як відомо властивість кутових коефіцієнтів двох перпендикулярних прямих \(k_1 = - \frac{1}{k_2} \)
Будуємо прямі на декартовій системі координат