Решение: Параллелограмм - это четырехугольник у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
В задании дано два уравнения прямых, определим являются ли они параллельными или нет:
Воспользуется свойством угловых коэффициентов параллельных прямых \(k_1=k_2\).
Найдем угловые коэффициенты прямых
\(3x-4y+16=0 => y = \frac{3}{4}x +4 => k_1 = \frac{3}{4} \)
\( 4x-y-11=0 => y = 4x-11 => k_2 = 4\)
получили \(k_1 \ne k_2\), т.е. прямые не являются параллельными.
Алгоритм дальнейшего решения:
1. Найдем точку пересечения прямых (сторон параллелограмма), координаты вершины A.
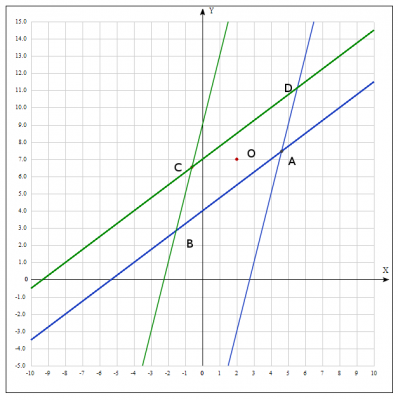
Решим систему уравнений $$ \begin{cases}3x-4y+16=0 \\4x-y-11=0\end{cases} => $$$$ \begin{cases}-13x+60=0 \\4x-y-11=0\end{cases} => \begin{cases} x = \frac{60}{13} \\ y = \frac{97}{13} \end{cases} $$ Подучили координаты точки \(A(\frac{60}{13}; \frac{97}{13}) => A(4.62; 7.46)\)
2. Найдем координаты вершины \(C(x_C;y_C)\), которая лежит на одной диагонали с вершиной A.
Нам известны одна из вершин параллелепипеда и точка пересечения диагоналей. Как известно, в точке пересечения диагонали делятся пополам, поэтому найдем координаты точки C (вторая вершина на этой диагонали). Координаты середины отрезка AC - точки O находятся по формуле \(O(\frac{x_A+x_C}{2};\frac{y_A+y_C}{2})\). Согласно условия задачи, координаты точки O(2;7), получаем
\(\frac{x_A+x_C}{2} = 2 => \frac{ \frac{60}{13}+x_C}{2} = 2 => x_C = - \frac{8}{13}\)
\(\frac{y_A+y_C}{2} = 7 => \frac{ \frac{97}{13}+x_C}{2} = 7 => y_C = \frac{85}{13}\)
Координаты искомой точки \(C(- \frac{8}{13};\frac{85}{13}) => C(- 0.62;6.54)\)
3. Найдем уравнения искомых прямых при известной координате одной точки и известных угловых коэффициентах.
Воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении $$ y - y_0 = k(x-x_0) \quad (1)$$
Найдем уравнение прямой CD, параллельной прямой \(y = \frac{3}{4}x +4 => k_1 = \frac{3}{4} \).
Подставляем координаты известной тоски \(C(- \frac{8}{13};\frac{85}{13})\) и значение углового коэффициента в (1), получаем
$$ y - \frac{85}{13} = \frac{3}{4}(x+\frac{8}{13}) => y = \frac{3}{4}x + 7$$
Найдем уравнение прямой BC, параллельной прямой \( y = 4x-11 => k_2 = 4 \).
Подставляем координаты известной тоски \(C(- \frac{8}{13};\frac{85}{13})\) и значение углового коэффициента в (1), получаем
$$ y - \frac{85}{13} = 4(x+\frac{8}{13}) => y = 4x + 9$$