Найти точку, симметричную точке Р(5;7) относительно прямой 5x+2y-9=0
Решение: точка, симметричная известной точке Р(5;7) относительно прямой 5x+2y-9=0 будет лежать на перпендикуляре, опущенном из точки P на прямую, т.е. будет лежать на прямой перпендикулярной известной прямой, проходящей через заданную точку.
Воспользуемся свойством перпендикулярных прямых - угловые коэффициенты перпендикулярных прямых связаны следующим соотношением $$k_1 = -\frac{1}{k_2} \quad (1)$$ рассмотрим прямую \(5x+2y-9=0 => y = \frac{9}{2} - \frac{5}{2}x\). Угловой коэффициент этой прямой равен \(k_1 = -\frac{5}{2} => k_2 = \frac{2}{5}\).
Для перпендикулярной прямой известны: координата точки Р(5;7) и угловой коэффициент \( k_2 = \frac{2}{5}\).
Найдем уравнение прямой, для этого применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении $$y - y_0 = k(x-x_0) \quad (2)$$ Подставляем координаты точки и значение углового коэффициента в (2) $$ y - 7 = \frac{2}{5}(x-5) => y = \frac{2}{5}x + 5$$ Известная точки P и искомая точка, назовем ее M, лежат на этой прямой, симметрично точке пересечения двух прямых O (эта точка делит отрезок PM пополам). Координаты центра отрезка точки \(O(x_O;y_O)\) находятся по формуле \(O( \frac{x_P+x_M}{2}; \frac{y_P+y_M}{2})\), тогда координаты искомой точки \(M(x_M;y_M) = M(2x_O - x_p; 2y_O-y_p) \quad (3)\).
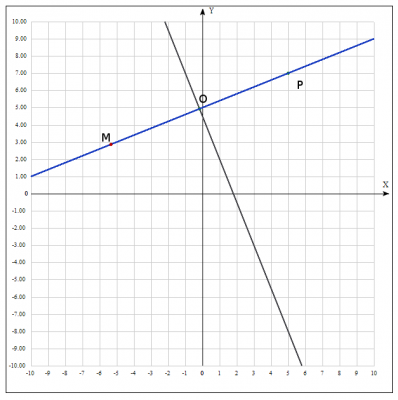
Найдем координаты точки \(O(x_O;y_O)\), как точки пересечения двух прямых, для этого решим систему уравнений $$\begin{cases}y = \frac{9}{2} - \frac{5}{2}x \\ y = \frac{2}{5}x + 5 \end{cases} => \begin{cases} x = -\frac{5}{29} \\ y = \frac{143}{29} \end{cases}$$ Получили координаты точки \(O(-\frac{5}{29};\frac{143}{29})\) Подставляем полученный координаты в (2) и найдем координат искомой точки \(M(x_M;y_M)\) $$ M(2x_O - x_p; 2y_O-y_p)=> M(2(-\frac{5}{29}) - 5; 2\frac{143}{29}-7) =>$$$$ M(-\frac{125}{29} ; \frac{83}{29}) $$ Для построения графика приближенные координаты точки равны \(M(-5.34 ; 2.86)\)