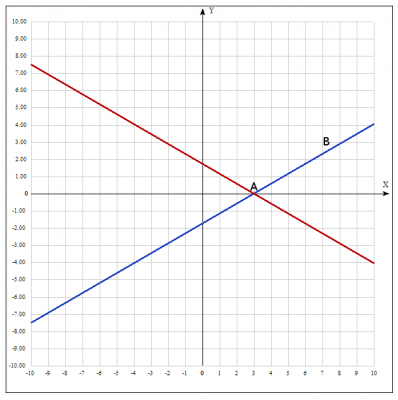
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ: —Ā–ĺ—Ā—ā–į–≤–ł–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ľ–ł–Ĺ–ł–ł, —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā –ļ–į–∂–ī–ĺ–Ļ —ā–ĺ—á–ļ–ł –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ī–ĺ —ā–ĺ—á–ļ–ł –ź(3;0) –≤ –ī–≤–į —Ä–į–∑–į –ī–į–Ľ—Ć—ą–Ķ —á–Ķ–ľ –ĺ—ā –ĺ—Ā–ł Ox.
–ü—É—Ā—ā—Ć B(x;y) - —ā–ĺ—á–ļ–į, –ļ–ĺ—ā–ĺ—Ä–į—Ź –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł—ā –ł—Ā–ļ–ĺ–ľ–ĺ–Ļ –ļ—Ä–ł–≤–ĺ–Ļ, –Ĺ–į–Ļ–ī–Ķ–ľ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ć—ā–ĺ–Ļ —ā–ĺ—á–ļ–ł
–ī–ĺ —ā–ĺ—á–ļ–ł –ź(3;0): –≤ –ī–Ķ–ļ–į—Ä—ā–ĺ–≤–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É —ā–ĺ—á–ļ–į–ľ–ł —Ä–į—Ā—Ā—á–ł—ā—č–≤–į–Ķ—ā—Ā—Ź –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ $$d = \sqrt{(x_2−x_1)^2+(y_2−y_1)^2} \quad (1)$$ –Ņ–ĺ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č –ł –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ $$d_1 = \sqrt{(x−3)^2+(y−0)^2}$$
–ī–ĺ –ĺ—Ā–ł Ox: —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł B(x;y) –ī–ĺ –ĺ—Ā–ł Ox —Ä–į–≤–Ĺ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ķ \(y\) —ć—ā–ĺ–Ļ —ā–ĺ—á–ļ–ł, –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ \(d_2=y\)
–°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ —É—Ā–Ľ–ĺ–≤–ł—Ź –∑–į–ī–į—á–ł, —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ī–ĺ —ā–ĺ—á–ļ–ł –ź(3;0) - \(d_1\) –≤ –ī–≤–į —Ä–į–∑–į –Ī–ĺ–Ľ—Ć—ą–Ķ, —á–Ķ–ľ –ī–ĺ –ĺ—Ā–ł Ox \(d_2\), —ā.–Ķ. \(d_1 = 2d_2 \quad (2)\)
–ü–ĺ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ–ľ –≤ (2) —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ: $$ \sqrt{(x−3)^2+y^2} =2y => (x−3)^2+y^2 = 4y^2 =>$$$$ (x−3)^2 = 3y^2 => y = \pm (\frac{1}{ \sqrt{3}}x−\sqrt{3}) $$
–ě—ā–≤–Ķ—ā: –Ņ–ĺ–Ľ—É—á–ł–Ľ–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ľ–Ķ—Ā—ā–ĺ —ā–ĺ—á–ļ–ł - –ī–≤–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –Ņ—Ä—Ź–ľ—č—Ö \(y = \pm (\frac{1}{ \sqrt{3}}x−\sqrt{3})\)