Функция \( y =\cos^2(x) - 2k\sin(x)\) - периодическая функция, а функция \( y = -4k-3\) - прямая, параллельная оси \(Ox\). Одна точка пересечения возможна только в точках максимума и минимума тригонометрической функции. Найдем эти точки, для этого найдем первую производную и приравняем к 0 $$y' =(\cos^2(x) - 2k\sin(x))' = -2\cos(x)*\sin(x) - 2k\cos(x) = 0 =>$$$$=\cos(x)(\sin(x) + k) = 0 =>$$$$\left[ \begin{gathered}\cos(x) = 0 \\ \sin(x) + k =0 \end{gathered}\right. =>\left[ \begin{gathered} x = \frac{\pi}{2} + \pi n \\ k = -\sin(x)\end{gathered}\right. $$Согласно условия задачи \(k\) - константа, поэтому будем рассматривать только случай \(x = \frac{\pi}{2} + \pi n\). В этих точках \(\cos(x) = 0\), а \(\sin(x) = \pm 1\), поэтому будем рассматривать два случая, приравняем обе функции при \(\sin(x) = 1\) и \(\sin(x) = -1\) и найдем соответствующие значения \(k\) $$\left[ \begin{gathered} -2k = -4k-3 \\ 2k = -4k-3 \end{gathered}\right. =>\left[ \begin{gathered} k = -\frac{3}{2} \\ k =-\frac{1}{2} \end{gathered}\right. $$Для проверки нашего решения построим графики функция
при \(k = -\frac{3}{2}\) функции примут вид \( y =\cos^2(x) + 3\sin(x)\), \(y = 3\)
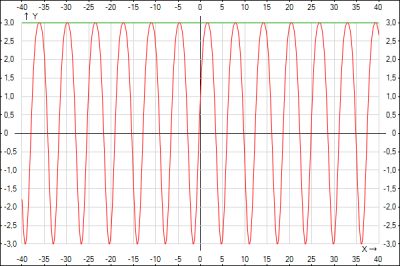
при \(k =-\frac{1}{2}\) функции примут вид \( y =\cos^2(x) + \sin(x)\), \(y = -1\)
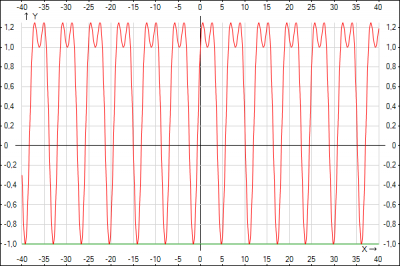
Из графиков видно истинность рассуждений.
Ответ: функции имеют одну точку касания при \(k = -\frac{3}{2} \) и \(k =-\frac{1}{2}\)



