Решение:
решим двумя способами:
1. Метод расстояний.
Найдем геометрической место точек, удовлетворяющее заданному условию. Пусть точка с координатами A(x;y) удовлетворяет этим условиям.
Расстояние от точки A(x;y) до оси Ox равно \(d = y\)
Расстояние от точки A(x;y) до фокуса F(2;2) равно \(d = \sqrt{(x-2)^2+(y-2)^2}\)
Приравняем эти расстояния $$ \sqrt{(x-2)^2+(y-2)^2} = y => (x-2)^2+(y-2)^2 = y^2 =>$$$$ (x-2)^2+ y^2-4y+4 = y^2 => y = \frac{1}{4}(x-2)^2+1 $$
2. Применим правило параболы.
вспомним определение: парабола - геометрическим местом точек, равноудаленных от точки, которая называется фокусом и заданной прямой, которая называется директрисой.
Мы вспомнили определение, чтобы понимать, какое уравнение мы должны получить.
Ищем уравнение параболы с фокусом в т. F(2;2) и директрисой - осью Ox.
1. Как мы помним уравнение параболы имеет вид $$x^2=2py$$ Параметр \(p\) равен расстоянию от фокуса до директрисы, т.е. от точки F(2;2) до оси Ox, получаем \(p=2\).
2. Точка пересечения параболы с осью Oy находится в т. \( y= 1\), по середине между директрисой и фокусом, т.е. парабола смещена вверх по оси Oy на \(y_0 = 1\)
3. Ось симметрии параболы равна \(x_0 = 2\)
Подставляем полученные данные и получаем уравнение параболы $$(x-x_0)^2=2p(y-y_0) => (x-2)^2=2*2(y-1) =>$$$$ y = \frac{1}{4}(x-2)^2 + 1$$
Проверка результатов.
Для проверки, выберем любую точку параболы и сравним расстояние от параболы до директрисы и фокуса.
Пусть \(x=2 => y=1\). Получили точку с координатами \((2;1)\).
Расстояние от точки до директрисы - оси Ox равно \(d = y =1\).
Расстояние от точки до фокуса найдем по формуле расстояния между точками \(d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\), получаем \( \sqrt{(2-2)^2+(2-1)^2} = 1\)
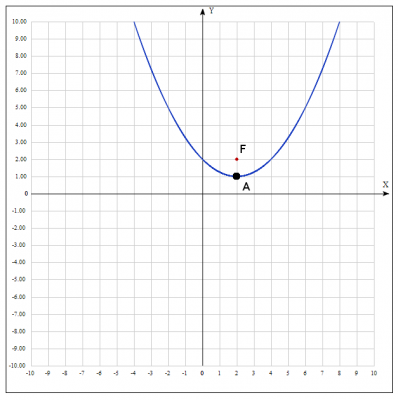
Построим параболу и убедимся в правильности решения.