Знайти координати центра ваги однорідної плоскої фігури ,обмеженої параболой \(y=\frac{1}{2}x^2\) та прямою \(y=4-x\)
Рішення:
теорія: якщо плоска фігура обмежена кривими \(y = f_1(x), \quad y=f_2(x) \), \(f_1(x) \leq f_2(x)\) і прямими \(x = a\) і \(x = b\), \(a \leq x \leq b\), то статичні моменти \(M_x\) і \(M_y\) плоскої фігури відносно осей Ox і Oy дорівнюють: $$M_x = \frac{1}{2}\int_a^b[f_2^2(x) - f_1^2(x)]dx $$$$ M_y = \int_a^bx[f_2(x) - f_1(x)]dx \quad (1)$$ Координати центра ваги криволінійної трапеції обчислюють за формулами: $$x_c = \frac{M_y}{S} = \frac{ \int_a^bx[f_2(x) - f_1(x)]dx}{S} $$$$ y_c = \frac{M_x}{S} = \frac{ \frac{1}{2}\int_a^b[f_2^2(x) - f_1^2(x)]dx}{S} \quad (2)$$ де \(S\) - площа криволінійної трапеції.
Алгоритм знаходження координат центру ваги.
1. Знаходимо площу криволінійної трапеції, обмеженої заданими кривими.
Фігура обмежена прямою \(y =4-x\) і параболою \(y =\frac{1}{2}x^2\), вітки якої направлені вгору, а координати вершини (0;0). Знайдемо точки перетину прямої і параболи, розв'язуючи систему $$\begin{cases}y =\frac{1}{2}x^2 \\y =4-x \end{cases} =>\begin{cases}x^2+2x-8 =0 \\y =4-x \end{cases} => $$$$ \begin{cases}x_1=-4;&x_2=2 \\y_1 =8;&y_2=2 \end{cases}$$ За двома знайденими точками будуємо пряму і за трьома точками - параболу.
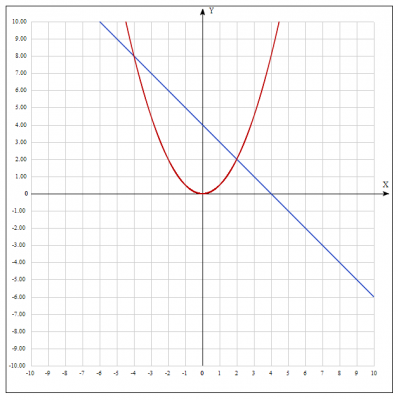
Точки перетину прямої і параболи визначають межі зміни змінної \(x\) . Отже \(x_1=-4; \quad x_2=2 \) - межі інтегрування.
Знайдемо шукану прощу за допомогою формули $$ S = \int_a^b(y_2-y_1)dx $$ отримуємо $$ S = \int_{-4}^2((4-x)-\frac{1}{2}x^2)dx = $$$$ = 4x-\frac{1}{2}x^2-\frac{1}{6}x^3|_{-4}^2=18 $$
2. Обчислимо статичні моменти фігури по формулі (1).
Врахуємо, що фігура обмежена неперервними кривими \(y_2 =4-x \quad y_1 = \frac{1}{2}x^2\), причому \( y_2 \geq y_1\)
$$M_x = \frac{1}{2}\int_{-4}^2[ (4-x)^2 - ( \frac{1}{2}x^2)^2]dx =$$$$ = 8x- 2x^2+\frac{1}{6}x^3 - \frac{1}{40}x^5|_{-4}^2 = \frac{288}{5}$$
$$M_y = \int_{-4}^2x[ 4-x - \frac{1}{2}x^2]dx =$$$$ = 2x^2- \frac{1}{3}x^3-\frac{1}{8}x^4|_{-4}^2 = -18$$
3. Обчислимо координати центра ваги по формулі (2).
$$x_c = \frac{M_y}{S} = \frac{ -18 }{18} = -1$$
$$y_c = \frac{M_x}{S} = \frac{ \frac{288}{5} }{18} = \frac{16}{5}$$
Відповідь: координати центра ваги однорідної плоскої фігури ,обмеженої параболой \(y=\frac{1}{2}x^2\) та прямою \(y=4-x\): \((-1;\frac{16}{5}) \)



