Решение: Эта задача на нахождение локального максимума (экстремума) вида "найти наибольший объем (площадь, длину и т.д.)".
Решение задачи сводится к нахождению функции (в данном случае объем) от одной переменной, а далее действуем по алгоритму нахождения экстремума.
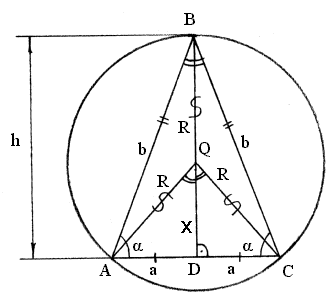
Решаем: опустим высоту \(h = BD\) (которая является также медианой) на основание равнобедренного треугольника \(a = AC\). Будем вращать фигуру вокруг основания \(AC\). Высота будет описывать наибольший круг. Фигура вращения - два конуса с основанием - круг, который описывает высота \(h\). Объем конуса будем искать по формуле $$ V_{конус} = \frac{1}{3}S_{осн}H $$ где \(S\) - площадь основания, в сновании круг, площадь которого рассчитывается как \(S_{осн} = \pi r^2\)
\(H\) - высота конуса.
Получаем объем пирамиды $$ V_{конус} = \frac{1}{3}\pi r^2H $$
Из рисунка видно, что высота конуса равна \(h = \frac{1}{2}a\) , получаем $$ V_{конус} = \frac{1}{3}\pi r^2\frac{1}{2}a $$ Фигура вращения состоит из двух конусов с равными объемами, т.е. нам нужно найти объем равный $$V = 2*V_{конус} = 2*\frac{1}{3}\pi r^2\frac{1}{2}a = \frac{1}{3}\pi r^2a$$
Получили формулу объема фигуры вращения, которая зависит от двух неизвестных \(r\) и \(a\), т.е. объем это функция двух переменных \(V(r,a)\). Найдем связь между этими переменными и получим функцию одной переменной.
Рассмотрим \(ΔABC\). Соединим центр круга и вершины треугольника, получим \(OA = OB=OC=R\). Обозначим \(OD=x\), т.е \(r = OB+OD = R+x\), где \(R = 3\) - радиус описанной окружности.
Рассмотрим прямоугольный треугольник \(ΔOCD\), применим теорему Пифагора \(OC^2 = OD^2+DC^2 => R^2 = x^2+(\frac{1}{2}a)^2 => a = 2\sqrt{R^2-x^2}\).
Подставляем в формулу объема $$ V = \frac{1}{3}\pi r^2a = \frac{1}{3}\pi (R+x)^22\sqrt{R^2-x^2}$$ Получили функцию одной переменной \(V(x) = \frac{1}{3}\pi (R+x)^2\sqrt{R^2-x^2}\).
Найдем наибольший объем, т.е. экстремум.
Найдем первую производную по переменной \(x\) и приравняем к 0. $$ V'(x) = \frac{1}{3}\pi [2(R+x)\sqrt{R^2-x^2} + (R+x)^2 \frac{1}{2\sqrt{R^2-x^2}}*(-2x)]$$ приравняем производную к 0 и проведем сокращение $$ \frac{1}{3}\pi [2(R+x)\sqrt{R^2-x^2} + (R+x)^2 \frac{1}{2\sqrt{R^2-x^2}}*(-2x)] = 0 => $$$$ (R+x) [2\sqrt{R^2-x^2} - (R+x)\frac{1}{\sqrt{R^2-x^2}}*x] = 0$$ по условию задачи \(R=3; \quad x > 0 \), т.е. \(R+x > 0\), получаем $$ 2\sqrt{R^2-x^2} - (R+x)\frac{1}{\sqrt{R^2-x^2}}*x = 0 =>$$ приравняем к общему знаменателю $$ \frac{2(R^2-x^2) - (R+x)x}{\sqrt{R^2-x^2}} = 0 => \frac{2(R-x) - x}{\sqrt{R^2-x^2}} = 0 =>$$$$ 2(R-x) - x = 0 => 2R-3x = 0 => x = \frac{2}{3}R = 2$$ проверяем, являемся ли значение \(x = 2\) - наибольшим значением. Найдем значение функции слева и справа от точки максимума
\( f(1) = \frac{1}{3}\pi (3+1)^2\sqrt{3^2-1^2} \approx 47.39 \)
\( f(2) = \frac{1}{3}\pi (3+2)^2\sqrt{3^2-2^2} \approx 58.54 \)
\( f(3) = \frac{1}{3}\pi (3+3)^2\sqrt{3^2-3^2} \approx 0 \)
Получили, что значение \(x = 2\), высота равнобедренного треугольника \(h\) равна \(h = R+x = 3+2=5\), при которой объем фигуры будет наибольшим.
Ответ: искомая высота треугольника при которой объем фигуры вращения будет наибольшим равна \(h = 5\)



