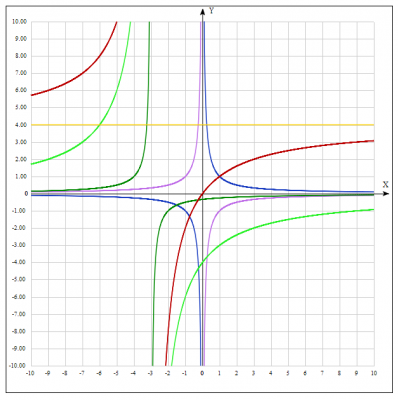
Решение: рассмотрим функцию \(y = \frac{4x}{x+3} \). Преобразуем ее методом выделения целой части в числителе $$y = \frac{4x}{x+3} => y = 4\frac{x+3-3}{x+3} => $$$$ y = 4 - \frac{12}{x+3}$$ получили уравнение гиперболы.
Исследуем функцию на непрерывность по следующему алгоритму:
1. Найти область определения функции:
Областью определения рациональной функции (дробь) будет: знаменатель не равен нулю, т.е. \( x +3 \ne 0 => x \ne -3 \) ОДЗ $$D_f=( -\infty; -3) \cup (-3;+\infty)$$
Получили в точке \(x=-3\) функция требует исследование на непрерывность, а в точке \(x = 1\) функция непрерывна и значение функции в этой точке \(f(1) = \frac{4x}{x+3} =1\)
2. Точки разрыва функции и их классификация. Функция имеет одну точку разрыва \(x = -3\)
исследуем точку \(x= -3\). Найдем предел функции справа и слева от точки разрыва, справа $$ \lim_{x \to -3+0} ( 4 - \frac{12}{x+3}) = -\infty $$ и слева от точки $$ \lim_{x \to -3-0} ( 4 - \frac{12}{x+3}) = \infty $$ Это точка разрыва второго рода т.к. односторонние пределы равны \( \infty\).
Прямая \(x = -3\) является вертикальной асимптотой.
3. вычислить предел функции при \( x \to \pm \infty\)
\( \lim_{x \to -\infty} ( 4 - \frac{12}{x+3}) = 4\)
\( \lim_{x \to +\infty} ( 4 - \frac{12}{x+3}) = 4\), получили, что
\(y=4\) - горизонтальная асимптота.
Определим как график функции приближается к асимптоте. Найдем пределы \( \lim_{ \pm \infty}(k - f(x))\), где \(y = k\) - горизонтальная асимптота
\( \lim_{x \to +\infty} ( 4 -(4 - \frac{12}{x+3})) = +0\) график функции приближается к асимптоте снизу.
\( \lim_{x \to -\infty} ( 4 -(4 - \frac{12}{x+3})) = -0\) график функции приближается к асимптоте сверху.
4. Нули функции (точки пересечения с осью Ox). Интервалы знакопостоянства функции.
Нули функции (точка пересечения с осью Ox): приравняем \(y=0\), получим \( \frac{4x}{x+3} = 0 => x = 0 \).
Кривая имеет одну точку пересечения с осью Ox с координатами \((0;0)\)
Интервалы знакопостоянства функции. На области определения функции \(( -\infty; -3) \cup (-3;+\infty)\) кривая имеет одну точку пересечения с осью Ox это \(x = 0\) , т.е. три интервала знакопостоянства
Определим знак функции на этих интервалах
интервал \(( -\infty; -3) \) найдем значение функции в любой точке \(f(-4) = \frac{4x}{x+3} > 0 \), на этом интервале функция отрицательная \(f(x) > 0 \), т.е. находится выше оси Ox.
интервал \(( -3; 0)\) найдем значение функции в любой точке \(f(-1) = \frac{4x}{x+3} < 0 \), на этом интервале функция отрицательная \(f(x) < 0 \), т.е. находится ниже оси Ox.
интервал \(( 0; \infty)\) найдем значение функции в любой точке \(f(1) = \frac{4x}{x+3} > 0 \), на этом интервале функция отрицательная \(f(x) > 0 \), т.е. находится выше оси Ox.
5. Точки пересечения с осью Oy:
приравняем \(x=0\), получим \( y = \frac{4x}{x+3} => y = 0 \). Получили одну точку пересечения с осью Oy с координатами (0;0)
6. Строим график функции \(y = 4 - \frac{12}{x+3}\).
Строить график будем схематически с использованием полученных результатом и элементарных преобразований.
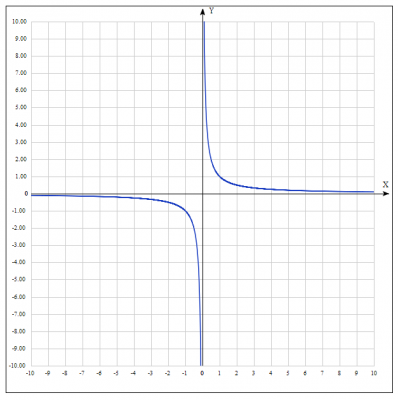
1. Строим простейший график функции \(y = \frac{1}{x}\) - гипербола, располагается в 1 и 3 четвертях
2. Строим простейший график функции \(y = -\frac{1}{x}\) путем симметричного отображения графика функции \(y = \frac{1}{x}\) относительно оси Oy.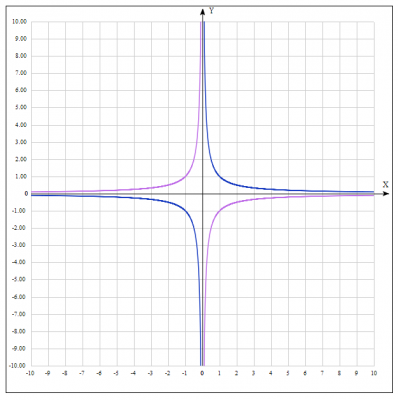
3. Строим простейший график функции \(y = -\frac{1}{x+3}\) путем сдвига графика функции \(y = -\frac{1}{x}\) на 3 влево вдоль оси Ox.
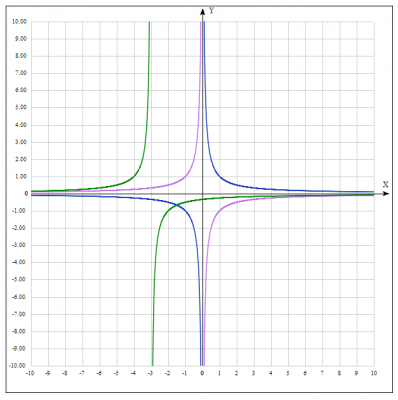
4. Строим простейший график функции \(y = -\frac{12}{x+3}\) путем растягивания графика функции \(y = -\frac{1}{x+3}\) по оси Oy.
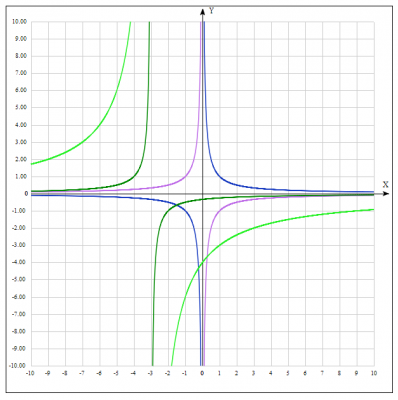
5. Строим простейший график функции \(y = 4 -\frac{12}{x+3}\) путем сдвига графика функции \(y = -\frac{12}{x+3}\) вдоль оси Oy на 4 вверх.