–†–Β―à–Β–Ϋ–Η–Β:
1. –ù–Α–Ι–¥–Β–Φ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―ç–Μ–Μ–Η–Ω―¹–Α, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–≥–Ψ ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ–Η A –Η B.
–Θ―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―ç–Μ–Μ–Η–Ω―¹–Α –Η–Φ–Β–Β―² –≤–Η–¥ \( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \). –£ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Η –Ϋ–Β–Η–Ζ–≤–Β―¹―²–Ϋ―΄ \(a;b\) - –Ω–Ψ–Μ―É–Ψ―¹–Η ―ç–Μ–Μ–Η–Ω―¹–Α. –ù–Α–Ι–¥–Β–Φ –Η―Ö, ―Ä–Β―à–Η–≤ ―¹–Η―¹―²–Β–Φ―É ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι. –£ –Ζ–Α–¥–Α–Ϋ–Η–Η ―¹–Κ–Α–Ζ–Α–Ϋ–Ψ, ―΅―²–Ψ ―ç–Μ–Μ–Η–Ω―¹ –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ –¥–≤–Β ―²–Ψ―΅–Κ–Η \( A( \sqrt{6};-2) B(-3; \sqrt{2})\). –ü–Ψ–¥―¹―²–Α–≤–Μ―è–Β–Φ –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ ―²–Ψ―΅–Β–Κ –≤ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Η ―Ä–Β―à–Α–Β–Φ –Ω–Ψ–Μ―É―΅–Β–Ϋ–Ϋ―É―é ―¹–Η―¹―²–Β–Φ―É –¥–≤―É―Ö ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι $$ \begin{cases} \frac{( \sqrt{6})^2}{a^2}+ \frac{(-2)^2}{b^2}=1\\ \frac{(-3)^2}{a^2}+\frac{(\sqrt{2})^2}{b^2} = 1 \end{cases} => \begin{cases} \frac{ 6}{a^2}+\frac{4}{b^2}=1\\ \frac{9}{a^2}+ \frac{2}{b^2}=1\end{cases} => $$$$ \begin{cases} \frac{ 6}{a^2}+ \frac{4}{b^2}=1\\ \frac{12}{a^2}=1 \end{cases} => \begin{cases}b = \sqrt{8} \\ a = \sqrt{12} \end{cases}$$
–ü–Ψ–¥―¹―²–Α–≤–Μ―è–Β–Φ –Ω–Ψ–Μ―É―΅–Β–Ϋ–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―²–Α –≤ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―ç–Μ–Μ–Η–Ω―¹–Α $$ \frac{x^2}{12}+\frac{y^2}{8}=1 $$ –Ω–Ψ–Μ―É―΅–Η–Μ–Η –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―ç–Μ–Μ–Η–Ω―¹–Α, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–≥–Ψ ―΅–Β―Ä–Β–Ζ –¥–≤–Β –Ζ–Α–¥–Α–Ϋ–Ϋ―΄–Β ―²–Ψ―΅–Κ–Η.
2. –ù–Α–Ι―²–Η –Ω–Ψ–Μ―É–Ψ―¹–Η, ―³–Ψ–Κ―É―¹―΄ –Η ―ç–Κ―¹―Ü–Β–Ϋ―²―Ä–Η―¹–Η―²–Β―² ―ç–Μ–Μ–Η–Ω―¹–Α.
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ –Ω–Ψ–Μ―É―΅–Β–Ϋ–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―ç–Μ–Μ–Η–Ω―¹–Α. \( \frac{x^2}{12}+\frac{y^2}{8}=1 \) –Η–Ζ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –≤–Η–¥–Ϋ–Ψ, –Ω–Ψ–Μ―É–Ψ―¹–Η ―ç–Μ–Μ–Η–Ω―¹–Α ―Ä–Α–≤–Ϋ―΄
\(a = \sqrt{12} \), \(b = \sqrt{8} \)
–ù–Α–Ι–¥–Β–Φ –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ ―³–Ψ–Κ―É―¹–Ψ–≤. –û–Ω―Ä–Β–¥–Β–Μ–Η–Φ, –Ϋ–Α –Κ–Α–Κ–Ψ–Ι –Ψ―¹–Η –Μ–Β–Ε–Η―² ―³–Ψ–Κ–Α–Μ―¨–Ϋ–Α―è –Ψ―¹―¨ \(F_1F_2\). –Δ.–Κ. a > b, ―²–Ψ ―³–Ψ–Κ–Α–Μ―¨–Ϋ–Α―è –Ψ―¹―¨ –Μ–Β–Ε–Η―² –Ϋ–Α (–≤–¥–Ψ–Μ―¨) –Ψ―¹–Η Ox, –Ω–Ψ―ç―²–Ψ–Φ―É –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ ―³–Ψ–Κ―É―¹–Ψ–≤ –±―É–¥―É―² ―¹–Μ–Β–¥―É―é―â–Η–Φ–Η: \(F_1(-c;0)\) –Η \(F_2(c;0)\), –≥–¥–Β \(c=\sqrt{a^2-b^2} => c=\sqrt{12-8}= 2\), ―².–Β. –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ ―³–Ψ–Κ―É―¹–Ψ–≤ –±―É–¥―É―² ―Ä–Α–≤–Ϋ―΄ \(F_1(-2;0)\) –Η \(F_2(2;0)\).
–ù–Α–Ι–¥–Β–Φ ―ç–Κ―¹―Ü–Β–Ϋ―²―Ä–Η―¹–Η―²–Β―² ―ç–Μ–Μ–Η–Ω―¹–Α.
–≠–Κ―¹―Ü–Β–Ϋ―²―Ä–Η―¹–Η―²–Β―² ―ç–Μ–Μ–Η–Ω―¹–Α ―Ä–Α―¹―¹―΅–Η―²―΄–≤–Α–Β―²―¹―è –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Β \(\epsilon = \frac{c}{a}\) => \(\epsilon = \frac{2}{ \sqrt{12}} = \frac{1}{ \sqrt{3}}\)
3. –ù–Α–Ι―²–Η –≤―¹–Β ―²–Ψ―΅–Κ–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è ―ç–Μ–Μ–Η–Ω―¹–Α ―¹ –Ζ–Α–¥–Α–Ϋ–Ϋ―΄–Φ –Κ―Ä―É–≥–Ψ–Φ.
–Γ–Ψ–≥–Μ–Α―¹–Ϋ–Ψ ―É―¹–Μ–Ψ–≤–Η―è –Ζ–Α–¥–Α―΅–Η, ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –≤ –Ϋ–Α―΅–Α–Μ–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―². –ö–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η \(x^2+y^2=R^2\). –ü–Ψ–¥―¹―²–Α–≤–Μ―è–Β–Φ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β ―Ä–Α–¥–Η―É―¹–Α –Η –Ω–Ψ–Μ―É―΅–Α–Β–Φ –Ζ–Α–¥–Α–Ϋ–Ϋ–Ψ–Β –≤ ―É―¹–Μ–Ψ–≤–Η–Η –Ζ–Α–¥–Α―΅–Η ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η $$x^2+y^2=3^2$$
–ù–Α–Ι–¥–Β–Φ ―²–Ψ―΅–Κ–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Η ―ç–Μ–Μ–Η–Ω―¹–Α, –¥–Μ―è ―ç―²–Ψ–≥–Ψ ―Ä–Β―à–Η–Φ ―¹–Η―¹―²–Β–Φ―É ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι $$ \begin{cases}x^2+y^2=3^2 \\\frac{x^2}{12}+\frac{y^2}{8}=1\end{cases} => $$$$ \begin{cases}x^2+y^2=9 \\x^2+\frac{3}{2}y^2=12\end{cases} => \begin{cases}x^2+y^2=9 \\ \frac{1}{2}y^2=3\end{cases}=> $$$$ \begin{cases}x = \pm \sqrt{3} \\ y= \pm \sqrt{6}\end{cases}$$
–ü–Ψ–Μ―É―΅–Η–Μ–Η 4 ―²–Ψ―΅–Κ–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Η ―ç–Μ–Μ–Η–Ω―¹–Α
\((-\sqrt{3};-\sqrt{6})\), \((-\sqrt{3};\sqrt{6})\), \((\sqrt{3};-\sqrt{6})\), \((\sqrt{3};\sqrt{6})\)
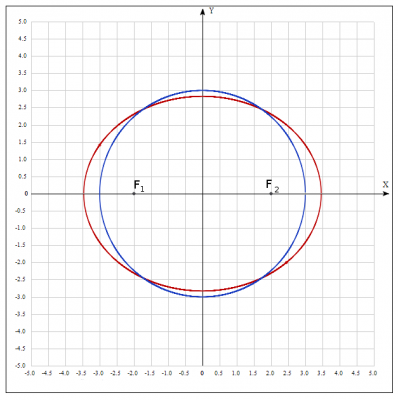
4. –ü–Ψ―¹―²―Ä–Ψ–Η―²―¨ ―ç–Μ–Μ–Η–Ω―¹ –Η –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨.