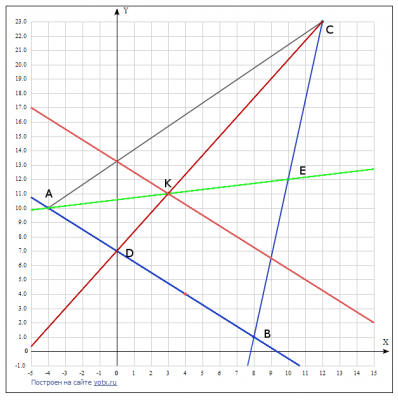
3. —É–≥–ĺ–Ľ –í –≤ —Ä–į–ī–ł–į–Ĺ–į—Ö —Ā —ā–ĺ—á–Ĺ–ĺ—Ā—ā—Ć—é –ī–ĺ –ī–≤—É—Ö –∑–Ĺ–į–ļ–ĺ–≤
–£–≥–ĺ–Ľ B - —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –Ņ—Ä—Ź–ľ—č–ľ–ł AB –ł BC - \(\angle ABC = \beta \) –Ī—É–ī–Ķ–ľ –ł—Ā–ļ–į—ā—Ć –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ $$ tg \beta = |\frac{k_2-k_1}{1+k_1k_2}| \quad (3)$$ –≥–ī–Ķ \(k_1,k_2\) - —É–≥–Ľ–ĺ–≤—č–Ķ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –Ņ—Ä—Ź–ľ—č—Ö \(k_{AB} = -\frac{3}{4} \quad k_{BC} = \frac{11}{2} \), –Ņ–ĺ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ–ľ –≤ (3) $$tg \beta = |\frac{ \frac{11}{2} + \frac{3}{4}}{1-\frac{11}{2}\frac{3}{4} }| = 2 => \beta = 1.11 —Ä–į–ī$$
–ě—ā–≤–Ķ—ā: —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –Ņ—Ä—Ź–ľ—č–ľ–ł AB –ł BC —Ä–į–≤–Ķ–Ĺ \( \angle \beta = 1.11 —Ä–į–ī\)
4. —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –≤—č—Ā–ĺ—ā—č –°D –ł –Ķ–Ķ –ī–Ľ–ł–Ĺ—É;
–≤—č—Ā–ĺ—ā–į –°D —Ä–į–≤–Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—é –ĺ—ā —ā–ĺ—á–ļ–ł C –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ AB, –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł–ľ —Ą–ĺ—Ä–ľ—É–Ľ—É —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā —ā–ĺ—á–ļ–ł –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ $$d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \quad (4)$$ –≥–ī–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ \(Ax+By+C=0\) - —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ –≤ –ĺ–Ī—Č–Ķ–ľ –≤–ł–ī–Ķ, –į \(x_0;y_0\) - –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł, —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ —Ä–į–≤–Ĺ–ĺ \(d\), –≤ –Ĺ–į—ą–Ķ–ľ —Ā–Ľ—É—á–į–Ķ —ć—ā–ĺ C(12;23)
–ü–ĺ–Ľ—É—á–ł–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ AB –≤ –ĺ–Ī—Č–Ķ–ľ –≤–ł–ī–Ķ \( y = 7 - \frac{3}{4}x => \frac{3}{4}x + y - 7 =0\). –ü–ĺ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ –ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł –≤ —Ą–ĺ—Ä–ľ—É–Ľ—É (4) $$d_{CD} = \frac{| \frac{3}{4}*12 + 1*23 - 7|}{\sqrt{(\frac{3}{4})^2+1^2}} = 20$$
–ě—ā–≤–Ķ—ā: –ī–Ľ–ł–Ĺ–į –≤—č—Ā–ĺ—ā—č CD —Ä–į–≤–Ĺ–į \(d = 20\)
—É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –≤—č—Ā–ĺ—ā—č CD
–Ě–į–Ļ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ CD, –ļ–ĺ—ā–ĺ—Ä–į—Ź –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–į AB. –í–ĺ—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—Ā—Ź —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ —É–≥–Ľ–ĺ–≤—č—Ö –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ĺ–≤ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č—Ö –Ņ—Ä—Ź–ľ—č—Ö $$k_1*k_2=-1 \quad (5)$$ –£–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –ĺ–ī–Ĺ–ĺ–Ļ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ \(k_{AB} = -\frac{3}{4} => \) –ł–∑ —Ą–ĺ—Ä–ľ—É–Ľ—č (5) –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ —É–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ņ—Ä—Ź–ľ–ĺ–Ļ CD —Ä–į–≤–Ĺ—č–Ļ \(k_{CD} = \frac{4}{3}\).
–Ě–į–Ļ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ CD, –ī–Ľ—Ź —ć—ā–ĺ–≥–ĺ –≤–ĺ—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—Ā—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ–ľ –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ –∑–į–ī–į–Ĺ–Ĺ—É—é —ā–ĺ—á–ļ—É –≤ –∑–į–ī–į–Ĺ–Ĺ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł $$ y - y_0 = k(x - x_0) \quad (6)$$ –∑–į–ī–į–Ĺ–Ĺ–į—Ź —ā–ĺ—á–ļ–į C(12;23), –į –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ķ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ —ć—ā–ĺ —É–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā \(k_{CD} = \frac{4}{3}\), –Ņ–ĺ–Ľ—É—á–ł–ľ $$ y - 23 = \frac{4}{3}(x -12) => y = \frac{4}{3}x + 7$$
–ě—ā–≤–Ķ—ā: —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –≤—č—Ā–ĺ—ā—č CD \( y = \frac{4}{3}x + 7 \)
5. —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ľ–Ķ–ī–ł–į–Ĺ—č –ź–ē –ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł –ö –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź —ć—ā–ĺ–Ļ –ľ–Ķ–ī–ł–į–Ĺ—č —Ā –≤—č—Ā–ĺ—ā–ĺ–Ļ –°D;
–£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ľ–Ķ–ī–ł–į–Ĺ—č AE.
–Ē–Ľ—Ź –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –ľ–Ķ–ī–ł–į–Ĺ—č AE –Ķ—Ā—ā—Ć –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į –ĺ–ī–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–ł A(-4;10), –į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č –≤—ā–ĺ—Ä–ĺ–Ļ —ā–ĺ—á–ļ–ł –Ņ—Ä—Ź–ľ–ĺ–Ļ E –Ĺ–į–Ļ–ī–Ķ–ľ –ļ–į–ļ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č –ĺ—ā—Ä–Ķ–∑–ļ–į \(BC\), –≥–ī–Ķ B(8;1) C(12;23) –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ \( E(\frac{x_B+x_C}{2};\frac{y_B+y_C}{2})\) => \( E(\frac{8+12}{2};\frac{1+23}{2}) \) => \( E( 10; 12) \)
–Ě–į—Ö–ĺ–ī–ł–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ \(AE\) –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ –ī–≤–Ķ –∑–į–ī–į–Ĺ–Ĺ—č–Ķ —ā–ĺ—á–ļ–ł \(A\) –ł \(E\) —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ (1)$$ \frac{x+4}{10+4}=\frac{y-10}{12-10} => y = \frac{1}{7}x + \frac{74}{7}$$
–ě—ā–≤–Ķ—ā: —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ľ–Ķ–ī–ł–į–Ĺ—č \( y = \frac{1}{7}x + \frac{74}{7}\)
–ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł –ö –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź —ć—ā–ĺ–Ļ –ľ–Ķ–ī–ł–į–Ĺ—č —Ā –≤—č—Ā–ĺ—ā–ĺ–Ļ –°D
–Ě–į–Ļ–ī–Ķ–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź K –≤—č—Ā–ĺ—ā—č CD –ł –ľ–Ķ–ī–ł–į–Ĺ—č AE, —Ā–ĺ—Ā—ā–į–≤–ł–ľ —Ā–ł—Ā—ā–Ķ–ľ—É —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ $$\begin{cases} y = \frac{4}{3}x + 7 \\ y = \frac{1}{7}x + \frac{74}{7} \end{cases} => \begin{cases} x =3 \\y = 11 \end{cases} $$
–ě—ā–≤–Ķ—ā: –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź K –≤—č—Ā–ĺ—ā—č CD –ł –ľ–Ķ–ī–ł–į–Ĺ—č AE \(K(3;11)\)
6. —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É –ö –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ –ź–í;
–í–ĺ—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—Ā—Ź —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ —É–≥–Ľ–ĺ–≤—č—Ö –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ĺ–≤ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č—Ö –Ņ—Ä—Ź–ľ—č—Ö $$k_1=k_2 \quad (7)$$ –£–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–Ļ \(k_{AB} = -\frac{3}{4} => \).
–Ě–į–Ļ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ł—Ā–ļ–ĺ–ľ–ĺ–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ , –ī–Ľ—Ź —ć—ā–ĺ–≥–ĺ –≤–ĺ—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—Ā—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ–ľ –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ –∑–į–ī–į–Ĺ–Ĺ—É—é —ā–ĺ—á–ļ—É –≤ –∑–į–ī–į–Ĺ–Ĺ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł $$ y - y_0 = k(x - x_0) $$ –∑–į–ī–į–Ĺ–Ĺ–į—Ź —ā–ĺ—á–ļ–į K(3;11), –į –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ķ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ —ć—ā–ĺ —É–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā \(k_2 = -\frac{3}{4}\), –Ņ–ĺ–Ľ—É—á–ł–ľ $$ y - 11 = -\frac{3}{4}(x - 3) => y = -\frac{3}{4}x + \frac{53}{4}$$
–ě—ā–≤–Ķ—ā: —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ , –ļ–ĺ—ā–ĺ—Ä–į—Ź –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AB –ł –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É K —Ä–į–≤–Ĺ–ĺ \(y = -\frac{3}{4}x + \frac{53}{4} \)
7. –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł –ú, —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ–Ļ –ļ —ā–ĺ—á–ļ–Ķ –ź –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ –°D
–Ę–ĺ—á–ļ–į A –Ľ–Ķ–∂–ł—ā –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AB, –ī–Ľ—Ź –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ł–∑–≤–Ķ—Ā—ā–Ĺ–į –≤—č—Ā–ĺ—ā–į CD, —ā–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —ā–ĺ—á–ļ–ł A –ł M –Ľ–Ķ–∂–į—ā –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AB —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –≤—č—Ā–ĺ—ā–į CD. –Ē–Ľ—Ź –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —ā–ĺ—á–ļ–ł M –Ĺ–į–Ļ–ī–Ķ–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł D, –ļ–į–ļ —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –ī–≤—É—Ö –Ņ—Ä—Ź–ľ—č—Ö AB –ł CD. –†–Ķ—ą–ł–ľ —Ā–ł—Ā—ā–Ķ–ľ—É —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ $$\begin{cases} y = 7 - \frac{3}{4}x \\y = \frac{4}{3}x + 7\end{cases} => \begin{cases} y = 7 \\x = 0\end{cases}$$ –Ĺ–į–Ļ–ī–Ķ–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł M, —Ä–Ķ—ą–ł–ľ —Ā–ł—Ā—ā–Ķ–ľ—É —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ $$\begin{cases}x_M = x_A + 2(x_D-x_A) \\ y_M = y_A + 2(y_D-y_A)\end{cases} =>\begin{cases}x_M = -4 + 2(0+4) \\ y_M = 10 + 2(7-10)\end{cases} => \begin{cases}x_M = 4 \\ y_M = 4 \end{cases} $$
–ě—ā–≤–Ķ—ā: –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł –ú, —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ–Ļ –ļ —ā–ĺ—á–ļ–Ķ –ź –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ –°D —Ä–į–≤–Ĺ—č M(4;4)