Решение: обозначим числа, которые мы будем выбирать как \(x,y,z\). Каждое из этих чисел будем откладывать на одноименной оси на отрезке [0;1]. Получаем, что выбранные три числа это точки в декартовой системе координат с координатами \((x,y,z)\) и которые попадают в куб с длиной ребра равной 1.
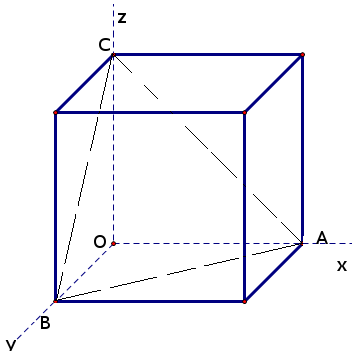
Согласно условия задачи мы должны найти вероятность для точек, для которых выполняется неравенство $$x+y+z \leq 1$$
Найдем координаты точек, сумма координат которых не превышает единицу.
Рассмотрим некоторые ключевые точки:
A если координаты \(y=z=0\), ко координата \(x \leq 1\), получаем координаты вершины \(A(1,0,0)\)
B если координаты \(x=z=0\), ко координата \(y \leq 1\), получаем координаты вершины \(B(0,1,0)\)
C если координаты \(x=y=0\), ко координата \(z \leq 1\), получаем координаты вершины \(C(0,0,1)\)
Рассмотрим плоскость, которая проходит через эти точки. Так как известны точки пересечения плоскости с осями, то уравнение этой плоскости в отрезках на осях равно $$ x+y+z = 1$$ а точки, сумма координат которых меньше 1, будут лежать ниже этой плоскости $$ x+y+z \leq 1$$ Получили, что искомые точки - точки, принадлежащие пирамиде \(OABC\), тогда искомая вероятность будет равна отношению объемов пирамиды и куба $$P = \frac{V_{пир}}{V_{куб}}$$ Объем куба равен \(V_{куб} =a^3\), т.к. длина ребра равна \(a=1 \) => \(V_{куб} = 1\)
Объем пирамиды равен \(V_{пир} =\frac{1}{3}S_{осн}H\), т.к. в основании лежит прямоугольный равнобедренный треугольник, то \(S_{осн} = \frac{1}{2}a^2\), а \(H=a=1\), получаем \(V_{пир} =\frac{1}{3}*\frac{1}{2}a^2*a = \frac{1}{6}a^3 = \frac{1}{6}\)
Вероятность того, что сумма чисел x,y,z будет не больше 1 равна $$P = \frac{V_{пир}}{V_{куб}} = \frac{\frac{1}{6}}{1} = \frac{1}{6}$$
Ответ: вероятность того, что сумма чисел \(x+y+z \leq 1\) равна \(P= \frac{1}{6}\)



