Решение: Построить на плоскости область допустимых решений системы линейных неравенств и графически найти наименьшее и наибольшее значения целевой функции. $$\begin{cases}-3x_1+x_2 \leq3 \\ x_1+x_2 \geq3 \\ 2x_1+x_2 \geq4 \\ x_1 \geq1,x_2 \leq 5 \\ x_1 \geq 0,x_2\geq 0 \end{cases} \\z=-2x_1+x_2$$
Графический способ решения задачи целесообразно использовать, для задач с двумя переменными, которые записаны в симметричной форме, а также для задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.
В данном случае задача с двумя переменными.
Алгоритм решения задачи "геометрическая интерпретация задачи линейного программирования":
1. Построим на плоскости \(x_1OX_2\) область допустимых решений.
2. Выделим область неотрицательных решений.
3. Найдем координаты вершин области.
4. Построим семейство целевых функций.
5. Находим максимальное (минимальное) значение целевой функции.
1. Строим область допустимых решений задачи \(D\).
Для построения области допустимых решений:
1) Строим граничные прямые:
преобразуем неравенства к равенствам, а затем к уравнению прямой линии в отрезках на осях вида \(\frac{x}{a}+\frac{y}{b} = 1\), тогда \(x=a\) - отрезок отсекаемый на оси Ox, \(y=b\) - на оси Oy $$\begin{cases} -3x_1+x_2 \leq 3 \\ x_1+x_2 \geq 3 \\ 2x_1+x_2 \geq 4 \\ x_1 \geq 1, x_2 \leq 5 \\ x_1 \geq 0,x_2\geq 0 \end{cases} => \begin{cases} -3x_1+x_2 = 3 \\ x_1+x_2 = 3 \\ 2x_1+x_2 = 4 \\ x_1 =1,x_2 = 5 \\ x_1 = 0,x_2 = 0 \end{cases} => \begin{cases} -x_1 + \frac{x_2}{3} = 1 \\ \frac{x_1}{3}+ \frac{x_2}{3} = 1 \\ \frac{x_1}{2} + \frac{x_2}{4} = 1 \\ x_1 =1,x_2 = 5 \\ x_1 = 0,x_2 = 0 \end{cases} $$ Для каждой прямой откладываем отрезки на осях и соединяем их. Получили нужные прямые.
2) Находим полуплоскости, которые удовлетворяют заданным неравенствам:
Для неравенства \( -3x_1+x_2 \leq 3 \) - полуплоскость, которая лежит ниже прямой \( -3x_1+x_2 = 3 \).
Для неравенства \( x_1+x_2 \geq 3 \)- полуплоскость, которая лежит выше прямой \( x_1+x_2= 3 \).
Для неравенства \( 2x_1+x_2 \geq 4 \)- полуплоскость, которая лежит выше прямой \( 2x_1+x_2 = 4 \).
Для неравенства \( x_1 \geq 1 \)- полуплоскость, которая лежит правее прямой \( x_1 = 1 \).
Для неравенства \( x_2 \leq 5 \)- полуплоскость, которая лежит ниже прямой \( x_2 = 5 \).
Область допустимых решений определяется как общая часть шести полуплоскостей, соответствующих данным неравенствам. Эта область представляет собой многоугольную неограниченную область
Областью \(D\) многоугольную неограниченную область \(ABCDE\) см. рис.
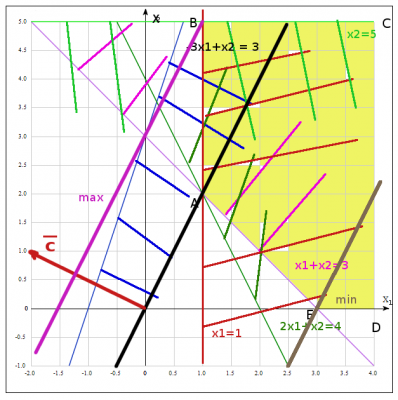
2.Выделим область неотрицательных решений.
Область неотрицательных решений расположена в первой четверти и является частью области \(D\), полученная из неравенств и дополнительно двух неравенства \(x_1 \geq 0 \) - верхняя полуплоскость (I и II четверти) и \( x_2 \geq 0\) - правая полуплоскость (I и IV четверти), которые выражают условие неотрицательности переменных \(x_1;x_2\), получили первую четверть. Получили искомую область неотрицательных решений \(ABCDE\) (закрашена).
3.Найдем координаты вершин области.
Координаты трех вершин уже известны (это точки пересечения прямых с осями).
Запишем эти координаты:
точка \(B(1;5)\),
точка \(A\) - точка пересечения трех прямых, одна из которых \(x_1=1\). Подставляем эту координату в уравнение одной их пересекающихся прямых и получим вторую координату \(x_1=1; \quad x_1+x_2=3 => x_2=2\), получили координаты точки \(A(1;2)\)
точка \(E\) - точка пересечения прямой \( x_1+x_2= 3 \) с осью \(x_2\) => \(x_1=3\), т.е. получили координаты \(E(3;0)\)
4. Строим семейство целевых функций.
Уравнение \( z=-2x_1+x_2 \rightarrow max,min\) определяет на плоскости \(x_1Ox_2\) семейство параллельных прямых, каждой из которых отвечает определенной значение параметра \(z\). Изветстно, что общее уравнение прямой на плоскости имеет вид \(Ax+By+C=0\), где координаты \((A;B)\) - координаты вектора нормали к прямой. Из условия задачи получаем \(z=-2x_1+x_2 \), т.е. координаты вектора нормали \(\vec{c} = (-2;1)\). Вектор нормали указывает направление наискорейшего возрастания параметра \(z\), а противоположный вектора \(-\vec{c}\) - направление наискорейшего убывания.
Строим прямую целевой функции при \(z=0 => x_2 = 2x_1\), строим вектор \(\vec{c}=(-2;1)\) (см рис. прямая черная, нормаль красная)
Задача определения точки максимума (минимума) точки \(z\) сведется к нахождению в допустимой области точки, через которую проходит прямая семейства \(z=const\), отвечающая за максимальное (минимальное) значение параметра \(z\).
5. Находим максимальное (минимальное) значение целевой функции.
Максимальное значение целевой функции: Найдем точку максимума путем параллельного переноса вспомогательной прямой \(z=0\) в направлении вектора \( \vec{c}\). Искомой точкой максимума является точка \(B(1;5)\) (см. розовая прямая)
Минимальное значение целевой функции: Найдем точку минимума путем параллельного переноса вспомогательной прямой \(z=0\) в направлении вектора \( -\vec{c}\). Искомой точкой минимума является точка \(E(3;0)\) (см. коричневая прямая)
Можно убедиться в правильности решения путем подстановки координат вершин в уравнение целевой функции:
в вершине \(B(1;5)\) значение целевой функции равно \( z(1;5)= -2*1+5 = 3\)
в вершине \(E(3;0)\) значение целевой функции равно \( z(3;0)= -2*3+0 = -6\)
Ответ:
Получили, что
минимальное значение целевой функции \( z_{min} = -6\)
максимальное значение целевой функции \( z_{max} = 3\)



