Решение:
1. Уравнения стороны AB треугольника.
Даны три вершины треугольника A(-2;-4), B(-1;4), C(3;3) , поэтому уравнения стороны будем искать при помощи формулы уравнения прямой, проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (1) \) Подставляем координаты вершин:
уравнение стороны AB, при известных координатах вершины A(-2;-4), B(-1;4) $$ AB \quad \frac{x+2}{-1+2} = \frac{y+4}{4+4} => y = 8x +12 $$
Ответ: уравнение стороны \(AB\): \(y = 8x +12\)
уравнение стороны BC, при известных координатах вершины B(-1;4), C(3;3) $$ BC \quad \frac{x+1}{3+1} = \frac{y-4}{3-4} => y = \frac{15}{4} - \frac{1}{4}x$$
Ответ: уравнение стороны \(BC\): \( y = \frac{15}{4} - \frac{1}{4}x\)
уравнение стороны AC, при известных координатах вершины A(-2;-4), C(3;3) $$ AC \quad \frac{x+2}{3+2} = \frac{y+4}{3+4} => y = \frac{7}{5}x -\frac{6}{5}$$
Ответ: уравнение стороны \(AC\): \(y = \frac{7}{5}x -\frac{6}{5}\)
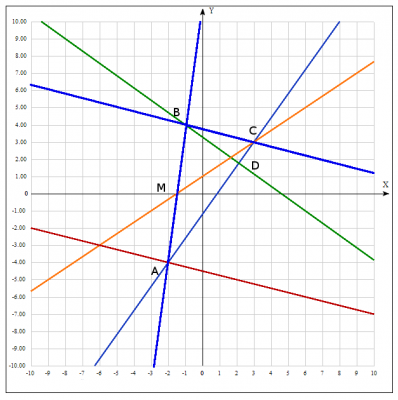
2. Угол В
Угол B - угол между прямыми AB и BC - \(\angle ABC = \beta \) будем искать по формуле $$ tg \beta = |\frac{k_2-k_1}{1+k_1k_2}| \quad (2)$$ где \(k_1,k_2\) - угловые коэффициенты прямых \(k_{AB} = 8 \quad k_{BC} = -\frac{1}{4} \), подставляем в (2) $$tg \beta = |\frac{ 8 + \frac{1}{4}}{1-8\frac{1}{4} }| = \frac{33}{4} => \beta \approx 83.09^0$$
Ответ: угол B между прямыми AB и BC равен \( \angle \beta \approx 83.09^0\)
3. Уравнение высоты BD, опущенной из вершины \(B\) на сторону \(AC\).
Высота BD опущена из вершины B на сторону AC, т.е. из условия известна одна координата точки B(-1;4) и направление - прямая перпендикулярна прямой AC. Воспользуемся свойством угловых коэффициентов перпендикулярных прямых: \(k_1 = -\frac{1}{k_2}\). Найдем угловой коэффициент \(k_1\) при \(k_2=k_{AC} = \frac{7}{5}\), получим \(k_{BD} = -\frac{1}{k_{BC}} = - \frac{5}{7} \). Найдем уравнение прямой BD, для этого воспользуемся уравнением прямой проходящей через заданную точку в заданном направлении $$ y - y_0 = k(x - x_0) \quad (3)$$ получим $$ y - 4 = - \frac{5}{7}(x + 1) => y = \frac{23}{7} -\frac{5}{7}x$$
Ответ: уравнение высоты BD \( y = \frac{23}{7} -\frac{5}{7}x \)
4. Уравнение медианы СМ, проведенную на сторону АВ.
Уравнение медианы CM.
Для нахождения медианы CM есть координата одной точки C(3;3), а координаты второй точки прямой M найдем как координаты середины отрезка \(AB\), где A(-2;-4), B(-1;4) по формуле \( M(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2})\) => \( M(\frac{-2-1}{2};\frac{-4+4}{2}) \) => \( M( -\frac{3}{2}; 0) \)
Находим уравнение прямой \(CM\) по формуле уравнения прямой, проходящей через две заданные точки \(A\) и \(E\) уравнение (1)$$ \frac{x-3}{-\frac{3}{2}-3}=\frac{y-3}{0-3} => y = \frac{2}{3}x + 1$$
Ответ: уравнение медианы \( y = \frac{2}{3}x + 1\)
5. Уравнение прямой, проведенную через точку А параллельно стороне ВС.
Прямая проходит точку \(A\), т.е. из условия известна одна координата точки A(-2;-4) и направление - прямая параллельна прямой BC \( y = \frac{15}{4} - \frac{1}{4}x\). Воспользуемся свойством угловых коэффициентов параллельных прямых: \(k_1 = k_2\). Найдем угловой коэффициент \(k_1\) при \(k_1 = k_2=k_{BC} = - \frac{1}{4} \). Найдем уравнение прямой BC, для этого воспользуемся уравнением прямой проходящей через заданную точку в заданном направлении $$ y - y_0 = k(x - x_0) \quad (3)$$ получим $$ y + 4 = - \frac{1}{4}(x + 2) => y = - \frac{1}{4}x - \frac{9}{2}$$
Ответ: уравнение прямой, проходящей через точку A и параллельна прямой стороны BC \( y = - \frac{1}{4}x - \frac{9}{2} \)
6. Длину высоты ВD
Длину высоту BD будем искать как расстояние от точки B до прямой AC по формуле $$ d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \quad (6)$$ где \((x_0;y_0)\) - координаты точки, а
\(Ax_0+By_0+C =0\) - общее уравнение прямой, расстояние до которой ищется.
Приводим уравнение прямой \(AC\) к общему виду \( y = \frac{7}{5}x -\frac{6}{5} => 7x -5y -6 = 0\), где \(A =7\), \(B = -5\), координаты точки B(-1;4) => \(x_0=-1;y_0=4\) подставляем в формулу (6) $$ d = \frac{|7*(-1) -5*4 -6|}{\sqrt{7^2+(-5)^2}} = \frac{33}{ \sqrt{74}} \approx 3,84$$
Ответ: длина высоты BD равна \(d \approx 3,84\)



