Построим график функции плотности распределения рис. 1.
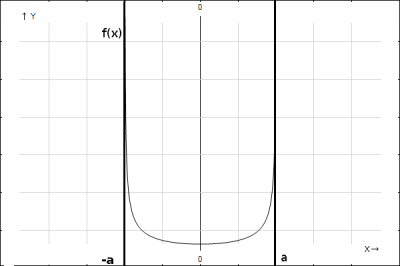
В теории вероятностей различают моменты двух видов: начальные и центральные моменты.
Начальным моментом \(k\)-го порядка случайной величины \(X\) называется математическое ожидание величины \(X^k\), т.е. $$\alpha_k = M[X^k]$$для непрерывной величины $$\alpha_k = \int_{-\infty}^{+\infty}x^kf(x) \, dx$$Из начальных моментов наиболее часто используют момент первого порядка $$\alpha = M[X] = m_x$$ это математическое ожидание. Найдем его $$M[X]= \int_{-\infty}^{+\infty}xf(x) \, dx =>$$$$M[X]= \int_{-a}^{a}x\frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx $$Найдем интеграл, для этого применим формулу Ньютона-Лейбница \(\int_a^bf(x)dx = F(b) - F(a)\), где \(F(x) = \int f(x)dx\). Найдем первообразную $$F(x) = \int x\frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx =$$применим замену переменной \(x = a\sin t => dx = a\cos t => t = \arcsin{\frac{x}{a}}\) $$ = \int a\sin t \frac{1}{\pi* \sqrt{a^2 - (a\sin t)^2}} \, a\cos t \, dt = \int a\sin t \frac{1}{\pi* a\sqrt{1 - \sin^2 t}} \, a\cos t \, dt = $$$$ \int a\sin t \frac{1}{\pi* a \cos t} \, a\cos t \, dt =\frac{a}{\pi} \int \sin t \, dt = -\frac{a}{\pi}*\cos t + C$$делаем обратную замену $$= -\frac{a}{\pi}*\cos \arcsin{\frac{x}{a}} + C = -\frac{a}{\pi}*\sqrt{1 - \sin^2 \arcsin{\frac{x}{a}}} + C =$$$$ = -\frac{a}{\pi}*\sqrt{1 - (\frac{x}{a})^2} + C = -\frac{1}{\pi}*\sqrt{a^2 - x^2} + C $$Подставляем функцию первообразной в определенный интеграл и получим $$m_x = M[X]= \int_{-a}^{a}x\frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx = $$$$ =-\frac{1}{\pi}*\sqrt{a^2 - x^2} |_{-a}^{a} = -\frac{1}{\pi}*\sqrt{a^2 - a^2} -( -\frac{1}{\pi}*\sqrt{a^2 - a^2}) = 0$$Получили математическое ожидание (иногда называют просто средним значением случайной величины \(X\)) \(m_x = M[X] = 0\). Из рисунка плотности распределения видно, что функция симметрична относительно оси \(Oy\), т.е математическое ожидание (средняя величина) должна быть равна 0, что мы и получили.
Начальные моменты высших порядков используются главным образом для вычисления центральных моментов.
Центральным моментом \(k\)-го порядка случайной величины \(X\) называют математическое ожидание величины \((X-m_x)^k\). Для непрерывной случайной величины $$\mu_k = \int_{-\infty}^{-\infty}(x-m_x)^kf(x) \, dx$$Среди центральных моментов часто используются - момент второго порядка $$D(x) = \int_{-\infty}^{\infty}(x-m_x)^2f(x) \,dx$$это дисперсия, найдем ее подставив функцию плотности распределения и математическое ожидание \(M[x] = m_x = 0\) $$D(x) = \int_{-a}^{a}x^2\frac{1}{\pi* \sqrt{a^2 - x^2}} \,dx$$опять воспользуемся формулой Ньютона-Лейбница, найдем неопределенный интеграл, а затем найдем разность значений первообразной на концах интервала. $$\int x^2\frac{1}{\pi* \sqrt{a^2 - x^2}} \,dx = $$введем замену \(x =a\sin(t) => dx = a\cos(t) => t = \arcsin{\frac{x}{a}}\)подставляем $$\int (a\sin(t))^2\frac{1}{\pi* \sqrt{a^2 - (a\sin(t))^2}} \,a\cos(t) \, dt = \int (a\sin(t))^2\frac{1}{\pi* a\cos(t)} \,a\cos(t) \, dt = \frac{a^2}{\pi} \int \sin^2(t) \, dt =$$вспомним формулу косинуса двойного угла \(\cos(2t) = \cos^2(t) - \sin^2(t) = 1 - 2\sin^2(t) => \sin^2(t) = \frac{1-\cos(2t)}{2}\) подставляем полученный результата в интеграл $$= \frac{a^2}{\pi} \int \frac{1-\cos(2t)}{2} \, dt = \frac{a^2}{\pi} *\frac{1}{2}t - \frac{a^2}{\pi}*\frac{1}{2} \int \cos(2t) \, dt =$$введем замену для интеграла\(u = 2t => du = 2dt => dt = \frac{du}{2}\) подставляем$$= \frac{a^2}{\pi} *\frac{1}{2}t - \frac{a^2}{\pi}*\frac{1}{2} \int \cos(u) \, \frac{du}{2} = \frac{a^2}{\pi} *\frac{1}{2}t + \frac{a^2}{\pi}*\frac{1}{2} \sin(u)*\frac{1}{2} = $$делаем обратную замену \(u = 2t\) $$ \frac{a^2}{\pi} *\frac{1}{2}t + \frac{a^2}{\pi}*\frac{1}{2} \sin(2t)*\frac{1}{2} =$$применяем формулу синуса двойного угла \(\sin(2t) = 2\sin(t)*\cos(t)\)$$= \frac{a^2}{\pi} *\frac{1}{2}t + \frac{a^2}{\pi}*\frac{1}{2} 2\sin(t)*\cos(t)\frac{1}{2} = \frac{a^2}{\pi} *\frac{1}{2}t + \frac{a^2}{\pi}*\frac{1}{2} \sin(t)*\sqrt{1 - \sin^2(t)} =$$делаем обратную замену \(t = \arcsin{\frac{x}{a}}\)$$= \frac{a^2}{\pi} *\frac{1}{2}\arcsin{\frac{x}{a}}+ \frac{a^2}{\pi}*\frac{1}{2} \sin(\arcsin{\frac{x}{a}})*\sqrt{1 - \sin^2(\arcsin{\frac{x}{a}})} =$$$$= \frac{a^2}{\pi} *\frac{1}{2}\arcsin{\frac{x}{a}}+ \frac{a^2}{\pi}*\frac{1}{2} \frac{x}{a}*\sqrt{1 - (\frac{x}{a})^2} = \frac{1}{2\pi} (a^2\arcsin{\frac{x}{a}} + x \sqrt{a^2 - x^2})$$Подставляем в формулу дисперсии и находим ее $$D(x) = \int_{-a}^{a}x^2\frac{1}{\pi* \sqrt{a^2 - x^2}} \,dx = \frac{1}{2\pi} (a^2\arcsin{\frac{x}{a}} + x \sqrt{a^2 - x^2}) |_{-a}^{a} =$$$$= \frac{1}{2\pi} (a^2\arcsin{\frac{a}{a}} + a \sqrt{a^2 - a^2}) - \frac{1}{2\pi} (a^2\arcsin{\frac{-a}{a}} + a \sqrt{a^2 - a^2}) =$$$$= \frac{1}{2\pi} a^2*\frac{\pi}{2} + \frac{1}{2\pi}a^2*\frac{\pi}{2} = \frac{1}{4} a^2 + \frac{1}{4}a^2 = \frac{1}{2}a^2$$Сразу же найдем среднеквадратическое отклонение $$\sigma_x = \sqrt{D(x)} = \sqrt{\frac{1}{2}a^2}=\frac{a}{\sqrt 2}$$Кроме полученных нами центрального момента второго порядка используются центральные моменты 3-го порядка \(\mu_3\), который является характеристикой симметрии функции плотности распределения, если функция симметрична \(\mu_3 = 0\). Центральные моменты 4-го порядка \(\mu_4\) используется для характеристики вершины распределения (острая или плоская).
Найдем вероятность \(Р(0 < Х < 2a)\).
Вероятность на указанном интервале равна площади фигуры, ограниченной графиком плотности распределения. Из графика плотности распределения видно, что при \(|x| >1, f(x) =0\), поэтому площадь равна 0. Ищем площадь на интервале \(0 < X < a\) $$Р(0 < Х < 2a) = \int_{0}^{2a} \frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx =$$$$ = \int_{0}^{a} \frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx + \int_{2}^{2a} \frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx =$$$$ = \int_{0}^{a} \frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx +0 = $$найдем неопределенный интеграл $$ \int \frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx =$$опят вводим замену \(x = a\sin(t) => dx = a\cos(t) dt=> t = \arcsin(\frac{x}{a})\) подставляем $$ = \int \frac{1}{\pi* \sqrt{a^2 - (a\sin(t))^2}} \, a\cos(t) dt = \int \frac{1}{\pi} \, dt = \frac{1}{\pi}t + C$$делаем обратную замену \(t = \arcsin(\frac{x}{a})\) подучили $$ = \frac{1}{\pi}\arcsin(\frac{x}{a})+ C$$Подставляем результата в определенный интеграл $$Р(0 < Х < 2a) = \int_{0}^{a} \frac{1}{\pi* \sqrt{a^2 - x^2}} \, dx =$$$$ = \frac{1}{\pi}\arcsin(\frac{x}{a}) |_{0}^{a} = \frac{1}{\pi}\arcsin(\frac{a}{a}) - \frac{1}{\pi}\arcsin(\frac{0}{a}) = $$$$ =\frac{1}{\pi}*\frac{\pi}{2} - 0 = \frac{1}{2}$$Проанализируем результат. Площади всей фигуры, ограниченной кривой плотности распределения равна 1 (вероятность достоверного события равна 1). График функции симметричен относительно оси \(Oy\), т.е. ось делит площадь на две равные части. Вывод, ответ получен правильный.



