Задание: вычислить объем тела, полученного вращением фигуры вокруг оси Ox, которая ограничена линиями
\( x= -y^2 + 6y + 4 \quad x - 5y - 2 = 0 \) , y = 0 при y > 0
Решение:
1. Построим кривые:
1.1. \( x= -y^2 + 6y + 4 \) - уравнение параболы.
Преобразуем уравнение параболы, выделим полный квадрат \( x= -y^2 + 6y + 4 => y^2 - 2*3y +9-9- 4 = -x \), \( (y -3)^2 = -x +13 => y = 3 \pm \sqrt{13-x}\)
1.2. \(x - 5y - 2 = 0 = > y = \frac{1}{5} x- \frac{2}{5} \) - уравнение прямой.
Рассмотрим рисунок:
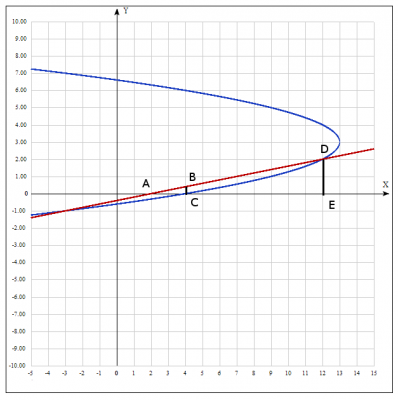
Нужно найти объем тела, полученного вращением \(ADC\) вокруг оси Ox.
2. Вычислить объем тела, полученного вращением фигуры вокруг оси Ox, которая ограничена линиями,
\(y = 0; \quad y > 0; \quad\), \( x= -y^2 + 6y + 4; \quad x - 5y - 2 = 0\).
Если тело получено путем вращения криволинейной трапеции, ограниченной кривой \(y_1 = f(x); y_2=g(x)\) (при этом \( 0 \leq f(x) \leq g(x)\)), осью абсцисс и прямыми \(x = a \) и \(x = b\) вокруг оси \(Ox\), объем рассчитывается по формуле $$V_x = \pi \int_a^b(y_2^2-y_1^2)dx \quad (1)$$
Из рисунка видно, что искомая фигура вращения состоит из двух фигур, ограниченных кривыми:
1. фигура вращения \(ABC \) ограничена кривыми $$ y_2 =\frac{1}{5} x- \frac{2}{5}; \quad y = 0$$
2. фигура вращения \( CBD\) ограничена кривыми $$ x - 5y - 2 = 0 => \quad y_2 =\frac{1}{5} x- \frac{2}{5} $$$$ x= -y^2 + 6y + 4 => \quad y_1 = 3 - \sqrt{13-x} $$
Искомый объем равен $$ V_{ADC} = V_{ABC} + V_{CBD} $$
Найдем объем \(V_{ABC}\)
Найдем границы
\(a\) - точка пересечения кривой \( x - 5y - 2 = 0 \) с осью Ox, получаем \(y = 0 => x = 2\)
\(b\) - точка пересечения кривой \( x= - y^2 + 6y + 4 \) с осью Ox, получаем \(y = 0 => x = 4\)
Кривая \(y_2 = \frac{1}{5} x- \frac{2}{5} \) и ось Оx \(y_1 = 0\)
Подставляем данные в формулу (1), получаем $$V_x = \pi \int_2^{4}( \frac{1}{5} x- \frac{2}{5})^2dx = \frac{8}{75}\pi $$
Найдем объем \(V_{CBD}\)
Найдем границы
\(a\) - точка пересечения кривой \( x= - y^2 + 6y + 4 \) с осью Ox, получаем \(y = 0 => x = 4\)
\(b\) - точка пересечения кривых, найдем ее, решив систему уравнений $$\begin{cases} x - 5y - 2 = 0 \\ x= -y^2 + 6y + 4 \\ y > 0 \end{cases} => \begin{cases} x - 5y - 2 = 0 \\ y_1=2; \quad y_2 = -1\\ y > 0 \end{cases} => $$$$ \begin{cases} x =12 \\ y = 2 \\ y > 0 \end{cases}$$ Получили \(a=2; \quad b=12\)
Подставляем данные в формулу (1), получаем $$V_x = \pi \int_4^{12}(( \frac{1}{5} x- \frac{2}{5})^2 - ( 3 - \sqrt{13-x})^2)dx = \frac{392}{75}\pi $$
Полный объем равен $$ V_{ADC} = V_{ABC} + V_{CBD} = \frac{8}{75}\pi + \frac{392}{75}\pi = \frac{16}{3} \pi$$
Ответ: объем тела, полученного вращением фигуры вокруг оси Ox, которая ограничена линиями \(y = 0; \quad y > 0; \quad\), \( x= -y^2 + 6y + 4; \quad x - 5y - 2 = 0\) равен \(V_{ADE} = \frac{16}{3}\pi\)



