Задание: найти площадь фигуры, ограниченной линиями \( x= y^2 + 6y + 4; \quad x - 7y - 10 = 0\)
Вычислить объем тела, полученного вращением фигуры вокруг оси Ox, которая ограничена линиями, y = 0 при y > 0
Решение:
1. найдем площадь фигуры, ограниченную кривыми \( x= y^2 + 6y + 4; \quad x - 7y - 10 = 0\)
Построим кривые:
1. \( x= y^2 + 6y + 4 \) - уравнение параболы.
2. \( x - 7y - 10 = 0 = > x = 7y + 10 \) - уравнение прямой.
Строим рисунок:
Нужно найти площадь криволинейной фигуры \(ABC\)
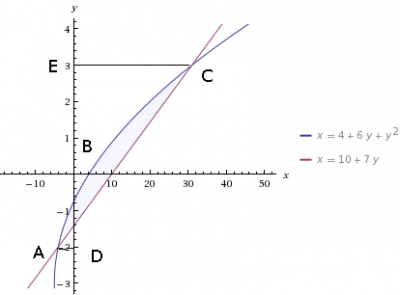
В данной задаче функции представлены в виде \(x = f(y)\), т.е. независимой переменной является \(y\)
Вспомним геометрический смысл определенного интеграла: если фигура ограниченна кривыми \(x_1=g(y)\) и \(x_2=f(y)\), причем функция \(f(y) > g(y)\), то определенный интеграл \(S = \int_a^b[f(y) - g(y)]dy\) равен площади фигуры этой фигуры.
Согласно условия задачи \(x_1= y^2 + 6y + 4; \quad x_2= 7y + 10 \), тогда искомая площадь фигуры \(ABC\) равна $$S_{ABC} = \int_D^E( 7y + 10 - (y^2 + 6y + 4))dy= \int_D^E( y - y^2 +6)dy$$ для нахождения интеграла нужно найти координаты \(y\) точек D и E. Это точки пересечения кривых, поэтому решим систему уравнений $$\begin{cases} x= y^2 + 6y + 4 \\ x= 7y + 10 \end{cases} => \begin{cases} y_1 = 3; y_2 = -2\\ x= 7y + 10 \end{cases} $$ Подставляем координаты \(y\) точек в интеграл $$S_{ABC} = \int_{-2}^{ 3}( y - y^2 +6)dy =$$ Для нахождения определенного интеграла, применим формулу Ньютона-Лейбница \(\int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a)\), получаем $$ = \frac{1}{2}y^2 - \frac{1}{3}y^3+6y|_{-2}^{3} = \frac{125}{6} \approx 20.833$$
Ответ: площадь фигуры, которая ограничена линиями \(x= y^2 + 6y + 4 \) и \( x= 7y + 10 \) равна \(S_{ABC} \approx 20.833 \)
2. Вычислить объем тела, полученного вращением фигуры вокруг оси Ox, которая ограничена линиями, \(y = 0; \quad y > 0; \quad x= y^2 + 6y + 4; \quad x - 7y - 10 = 0\).
Если тело получено путем вращения криволинейной трапеции, ограниченной кривой \(y_1 = f(x); y_2=g(x)\) (при этом \( 0 \leq f(x) \leq g(x)\)), осью абсцисс и прямыми \(x = a \) и \(x = b\) вокруг оси \(Ox\), объем рассчитывается по формуле $$V_x = \pi \int_a^b(y_2^2-y_1^2)dx \quad (1)$$
В задании фигура ограничена функцией $$ x= 7y + 10 => y = \frac{x}{7} - \frac{10}{7} ; \quad y_1 = \frac{x}{7} - \frac{10}{7} $$$$ x= y^2 + 6y + 4 => x= y^2 + 2*3y + 9 - 9+4 => $$$$x= (y+3)^2 - 5 => y = \pm \sqrt{x+5}-3 \quad y_2 = \pm \sqrt{x+5}-3 $$ согласно условия задачи \( y > 0\) => $$ y_2 = \sqrt{x+5}-3 $$
Границы
\(a\) - точка пересечения кривой \(x= y^2 + 6y + 4\) с осью Ox, т.е. \(y=0 => x=4\)
\(b\) - точка пересечения кривых, найдем ее, решив систему уравнений $$\begin{cases}x= y^2 + 6y + 4 \\ x= 7y + 10 \\ y > 0 \end{cases} => \begin{cases}y_1=3; \quad y=-2 \\ x= 7y + 10 \\ y > 0 \end{cases} => $$$$ \begin{cases} y=3 \\ x = 31 \\ y > 0 \end{cases}$$ Получили \(a=4; \quad b=31\)
Подставляем данные в формулу (1), получаем $$V_x = \pi \int_4^{31}((\sqrt{x+5}-3)^2 - (\frac{x}{7} - \frac{10}{7})^2)dx = $$$$ = \pi \int_4^{31}((x+5 - 6\sqrt{x+5}+9) - \frac{1}{49}(x^2 - 20x+100))dx = $$ применим формулу Ньютона-Лейбница \( \int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a) \), получим $$= \pi [( \frac{1}{2}x^2+14x - 4(x+5)^{\frac{3}{2}}) - \frac{1}{49}( \frac{x^3}{3} - 10x^2+100x)]|_4^{31} \approx 30\pi$$
Ответ: объем тела, полученного вращением фигуры вокруг оси Ox, которая ограничена линиями \(y = 0; \quad y > 0; \quad x= y^2 + 6y + 4; \quad x - 7y - 10 = 0\) равен \(V_x \approx 30\pi \)



