Решение: уравнения \(y=\sqrt{x}; \quad y=2\sqrt{x};\) - определяют на плоскости xOy две степенные функции, которые имеют общую вершину в точке начала координат. Две степенные функции пересекает прямая \(x=4\).
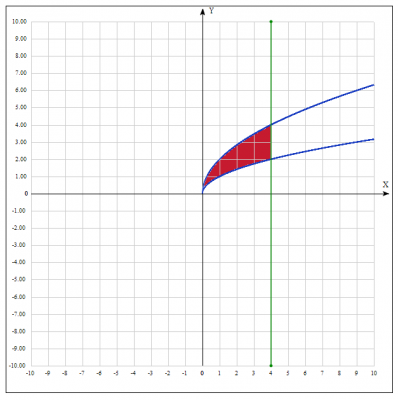
рисунок.
Обозначим площадь искомой области как \(D\). Чтобы найти площадь области \(D\), ограниченной заданными линиями, воспользуемся формулой $$\int_D\int dxdy$$
Можно взять внутренний интеграл по переменной \(y\), есть уравнения, связывающие \(y(x)\) , а внешний по переменной \(x\) (можно и наоборот, результат будет одинаковый), из условия задачи уже известны границы этой переменной \(x \in [0;4]\). Получаем $$ S_D = \int_0^4dx\int_{\sqrt{x}}^{2\sqrt{x}}dy = $$находим внутренний определенный интеграл $$ = \int_0^4(y|_{\sqrt{x}}^{2\sqrt{x}})dx = \int_0^4(2\sqrt{x} - \sqrt{x})dx = $$$$ = \int_0^4\sqrt{x}dx =$$ находим внешними интеграл $$ = \frac{1}{\frac{1}{2}+1}x^{\frac{1}{2}+1}|_0^4 = \frac{2}{3}(4^{\frac{3}{2}} - 0) = \frac{16}{3}$$
Ответ: площадь фигуры, ограниченная заданными линиями равна \(S_D = \frac{16}{3}\)



