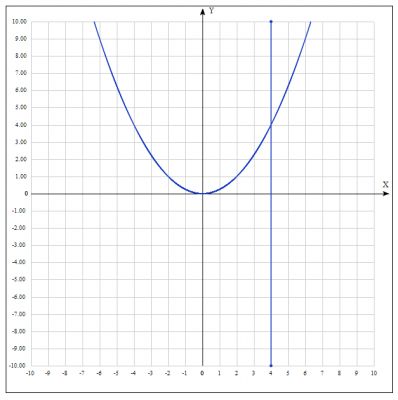
Решение: найдем объем фигуры, ограниченной степенной функцией с целой четной степенью \( y = \frac{1}{4}x^2\) (парабола), прямой \(x= 4\) вокруг оси Ox.
где \(x=4\) - прямая параллельная оси Oy
\(y = \frac{1}{4}x^2\) - парабола, ветви которой направлены вверх, вершина в точке (0;0).
Строим рисунок:
Если тело получено путем вращения криволинейной трапеции, ограниченной кривой \(y = f(x)\) (при этом \( f(x) \geq 0\)), осью абсцисс и прямыми \(x = a \) и \(x = b\) вокруг оси \(Ox\), объем рассчитывается по формуле $$V_x = \pi \int_a^by^2dx \quad (1)$$
В задании фигура ограничена функцией $$y = \frac{1}{4}x^2$$ Из рисунка следует что будем искать объем фигуры, образованной параболой, расположенной в первой четверти и прямой \(x=4\). Найдем границы \([a;b]\)
1. граница \(a\) - точка пересечения параболы с осью Ox (0;0)
2. граница \(b\) - прямая \(x=4\)
получили границы \([0;4]\)
Подставляем данные в формулу (1), получаем $$V_x = \pi \int_0^4( \frac{1}{4}x^2)^2dx = \frac{1}{16}\pi \int_0^4x^4dx =$$ применим формулу Ньютона-Лейбница \( \int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a) \), получим $$ = \frac{1}{16}\pi \frac{1}{5}x^5|_0^4 = \frac{1}{80}\pi ( 4^5-0^0 ) = \frac{64}{5}\pi$$
Ответ: объем тела, полученное путем вращения криволинейной трапеции равен \( V_x = \frac{64}{5}\pi\)



