Решение: найдем максимальное и минимальное значение функции \(f (x, y)\) при следующих ограничениях $$ f(x,y)=(x-4)^2 + (y-3)^2 \rightarrow max,min \\ \begin{cases} 2x+3y\geq 6 \\ 3x-2y\leq 18\\ -x+2y\leq 8\\ x,y\geq0\end{cases} $$
Графический способ решения задачи целесообразно использовать, для задач с двумя переменными, которые записаны в симметричной форме, а также для задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.
В данном случае задача с двумя переменными.
Алгоритм решения задачи "геометрическая интерпретация задачи линейного программирования":
1.Построим на плоскости xOy область допустимых решений.
2.Выделим область неотрицательных решений.
3.Найдем координаты вершин области.
4. Построим семейство целевых функций.
5. Находим максимальное (минимальное) значение целевой функции.
1. Строим область допустимых решений задачи \(D\).
Для построения области допустимых решений:
1) Строим граничные прямые:
преобразуем неравенства к равенствам, а затем к уравнению прямой линии в отрезках на осях вида \(\frac{x}{a}+\frac{y}{b} = 1\), тогда \(x=a\) - отрезок отсекаемый на оси Ox, \(y=b\) - на оси Oy $$ \begin{cases} 2x+3y = 6 \\ 3x-2y = 18\\ -x+2y = 8 \end{cases} => \begin{cases} \frac{x}{3}+\frac{y}{2} = 1 \\ \frac{x}{8}-\frac{y}{9} = 1 \\ -\frac{x}{6}+ \frac{y}{4} = 1 \end{cases} $$ Для каждой прямой откладываем отрезки на осях и соединяем их. Получили нужные прямые.
2) Находим полуплоскости, которые удовлетворяют заданным неравенствам:
Для неравенства \(2x+3y\geq 6\) - полуплоскость, которая лежит выше прямой \(2x+3y = 6\). Прямая AC
Для неравенства \(3x-2y\leq 18 => -3x+2y \geq -18\)- полуплоскость, которая лежит выше прямой \(3x-2y = 18\). Прямая CB
Для неравенства \(-x+2y\leq 8\)- полуплоскость, которая лежит ниже прямой \(-x+2y = 8\). Прямая AB
Область допустимых решений определяется как общая часть трех полуплоскостей, соответствующих данным неравенствам. Эта область представляет собой треугольник \(ABC\)
Областью \(D\) является треугольник \(ABC\) см. рис.
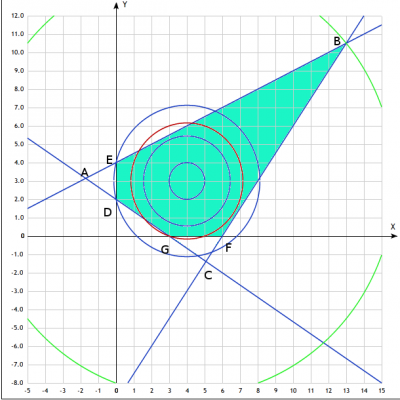
2.Выделим область неотрицательных решений.
Область неотрицательных решений расположена в первой четверти и является общей частью всех пяти полуплоскостей, три их которых - область \(D\), полученная из неравенств и дополнительно два неравенства \(x \geq 0\) - верхняя полуплоскость (I и II четверти) и \(y \geq 0\) - правая полуплоскость (I и IV четверти), которые выражают условие неотрицательности переменных \(x;y\). Получили искомую область неотрицательных решений \(DEBFG\)
3.Найдем координаты вершин области.
Координаты четырех вершин уже известны (это точки пересечения прямых с осями).
Запишем эти координаты:
\(D(0;2)\), \(E(0;4)\), \(F(6;0)\), \(G(3;0)\)
Найдем координаты точки \(B\), как точки пересечения прямых \(-x+2y = 8\) и \(3x-2y = 18\). Решим систему уравнений и найдем координаты этой точки $$\begin{cases} -x+2y = 8\\ 3x-2y = 18\end{cases}=> \begin{cases} 2x = 26\\ 3x-2y = 18\end{cases}=> \begin{cases} x = 13\\ y =10.5\end{cases}$$
Получили координаты точки \(B(13;10.5)\)
4. Строим семейство целевых функций.
Уравнение \( f(x,y)=(x-4)^2 + (y-3)^2 \rightarrow max,min\) определяет на плоскости xOy семейство концентрических окружностей с центом в точке с координатами \(Q(4;3)\), каждой из которых отвечает определенное значение параметра \(f\). Как известно, для уравнения окружности параметр \(f=R^2\).
Изобразим в одной системе координат семейство концентрических окружностей \(f\) и семейство прямых. Задача определения точки максимума (минимума) точки \(f\) сведется к нахождению в допустимой области точки, через которую проходит окружность семейства \(f=const\), отвечающая за наибольшее (наименьшее) значение параметра \(f\).
5. Находим максимальное (минимальное) значение целевой функции.
Минимальное значение целевой функции: Путем постепенного увеличения радиуса окружности мы получили, что первая вершина, через которую пройдет окружность это точка \(G(3;0)\). Целевая функция в этой точке будет минимальной и равна \( f(3,0)=(3-4)^2 + (0-3)^2 = 10\)
Максимальное значение целевой функции: Путем дальнейшего увеличения радиуса окружности мы получили, что последняя вершина, через которую пройдет окружность это точка \(B(13;10.5)\). Целевая функция в этой точке будет максимальной и равна \( f(13,10.5)=(13-4)^2 + (10.5-3)^2 = 137.25\)
Можно убедиться в правильности решения путем подстановки координат оставшихся вершин в уравнение целевой функции:
в вершине \(D(0;2)\) значение целевой функции равно \( f(0,2)=(0-4)^2 + (2-3)^2 = 17\)
в вершине \(E(0;4)\) значение целевой функции равно \( f(0,4)=(0-4)^2 + (4-3)^2 = 17\)
в вершине \(F(6;0)\) значение целевой функции равно \( f(6,4)=(6-4)^2 + (0-3)^2 = 13\)
Получили, что
минимальное значение целевой функции \(f_{min} = 10\)
максимальное значение целевой функции \(f_{max} = 137.25\)
Ответ:
минимальное значение целевой функции \(f_{min} = 10\)
максимальное значение целевой функции \(f_{max} = 137.25\)



