Решение:
1. Составим ряд распределения случайной величины \(X\) :
\(X\) - дискретная случайная величина равная числу неудачных экспериментов (промахов) в серии из 3 экспериментов, тогда \(X \in \text{{0,1,2,3}}\),
Составим закон распределения случайной величины (ряд распределения) в виде таблицы:
$$ \begin{array}{|c|c|c|}\hline x_i& 0& 1& 2& 3 \\ \hline \\ p_i& & & & \\ \hline \end{array} $$
Найдем вероятности случайных величин.
событие \(A_1\) - первый эксперимент удачный, а событие \(\overline{A_1}\) - неудачный, тогда \(P(A_1) = 0.9\), а \(P(\overline{A_1}) = 0.1\)
событие \(A_2\) - второй эксперимент удачный, а событие \(\overline{A_1}\) - неудачный, тогда \(P(A_2) = 0.8\), а \(P(\overline{A_2}) = 0.2\)
событие \(A_3\) - третий эксперимент удачный, а событие \(\overline{A_1}\) - неудачный, тогда \(P(A_3) = 0.7\), а \(P(\overline{A_3}) = 0.3\)
тогда случайная величина \(X = i\) равна
\(X=0; \quad A_1A_2A_3\) - нет неудачных экспериментов (промахов)
\(X=1; \quad A_1A_2 \overline{A_3} + A_1 \overline{A_2}A_3 + \overline{A_1}A_2A_3\) - один промах
\(X = 2; \quad A_1\overline{A_2}\overline{A_3} + \overline{A_1}A_2\overline{A_3} + \overline{A_1}\overline{A_2}A_3\) - два промаха
\(X =3; \quad \overline{A_1}\overline{A_2}\overline{A_3}\) - три промаха
Рассмотрим каждый случай отдельно и найдем его вероятность:
1. \(X=0\) нет промахов (три попадания)
$$ p(X=3) = p(A_1A_2A_3)= p(A_1)p(A_2)p(A_3)= 0.9*0.8*0.7 = 0.504$$
2. \(X=1\) один промах
$$ p(X=1) = p(A_1A_2 \overline{A_3} + A_1 \overline{A_2}A_3 + \overline{A_1}A_2A_3) = $$$$ = p(A_1A_2 \overline{A_3}) + p(A_1 \overline{A_2}A_3) + p(\overline{A_1}A_2A_3)= $$$$ = p(A_1)p(A_2)p(\overline{A_3}) + p(A_1)p(\overline{A_2})p(A_3) + p(\overline{A_1})p(A_2)p(A_3)= $$$$ = 0.9*0.8*0.3 + 0.9*0.2*0.7 + 0.1*0.8*0.7 = 0.398$$
3. \(X=2\) два промаха
$$p(X=2) = p(A_1\overline{A_2}\overline{A_3} + \overline{A_1}A_2\overline{A_3} + \overline{A_1}\overline{A_2}A_3) = $$$$ = p(A_1\overline{A_2}\overline{A_3}) + p(\overline{A_1}A_2\overline{A_3}) + p(\overline{A_1}\overline{A_2}A_3) = $$$$ = p(A_1)p(\overline{A_2})p(\overline{A_3}) + p(\overline{A_1})p(A_2)p(\overline{A_3}) + p(\overline{A_1})p(\overline{A_2})p(A_3) = $$$$ = 0.9*0.2*0.3 + 0.1*0.8*0.3 + 0.1*0.2*0.7 = 0.092$$
4. \(X=3\) три промаха
$$p(X=3) = p(\overline{A_1}\overline{A_2}\overline{A_3}) = p(\overline{A_1})p(\overline{A_2})p(\overline{A_3}) = 0.1*0.2*0.3 = 0.006$$
Проверяем результат: так как все события \(X \in \text{{0,1,2,3}}\) образуют полную группу событий, то сумма вероятностей должна быть равна 1, т.е. \(p(X=0) + p(X=1) + p(X=2) + p(X=3) = \) \( = 0.504 + 0.398 + 0.092 + 0.006 = 1 \)
расчеты проведены правильно, заполняем таблицу
$$ \begin{array}{|c|c|c|}\hline X & 0& 1& 2& 3 \\ \hline \\ p(X=i)& 0.504 & 0.398 & 0.092 & 0.006 \\ \hline \end{array} $$
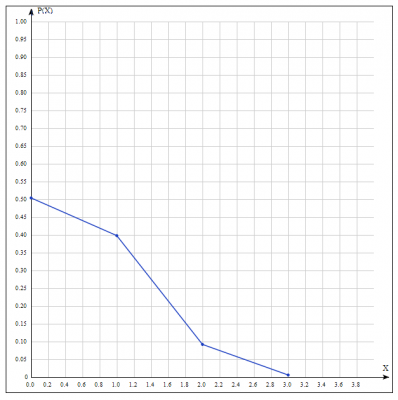
2. Полигон распределения
Для построения полигона распределения (см.рис.) по оси абсцисс (X) откладываем количественные значения варьирующего признака (случайная величина \(X = {0;1;2;3}\) ) — варианты, а по оси ординат — частоты или части (в данном случае вероятности \(p(X=i)\))