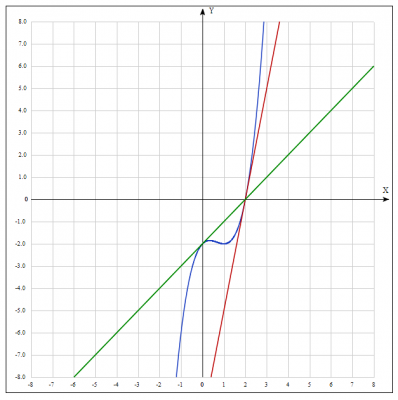
Задание: найти уравнение касательной к графику функции \(y=(x^2+1)(x-2)\) в точках пересечения с осями координат.
Решение: уравнение касательной в точке равно $$y = f(x_0) + f'(x_0)(x-x_0) \quad (1)$$ В задании координаты точек касания нам не даны, но их можно найти из условия, что касательная проходит в точках пересечения с осями координат. Найдем координаты точек пересечения.
1. точка пересечения с осью Ox: в этих точках координата \(y=0\), найдем координаты \(x\), \((x^2+1)(x-2) = 0 => x=2\). Координаты пересечения с осью Ox (2;0)
2. точка пересечения с осью Oy: в этих точках координата \(x=0\), найдем координаты \(y\), \(y(0) = (0^2+1)(0-2) => y= -2\). Координаты пересечения с осью Oy (0;-2)
Получили координаты двух точек касания, найдем уравнения касательных в этих точках.
Найдем первую производную функции \(y=(x^2+1)(x-2) = x^3-2x^2+x-2\)
$$y' = (x^3-2x^2+x-2)' = 3x^2-4x+1$$
1. Уравнения касательных в точке с координатами (2;0)
Найдем значение производной функции в точке \(x_0=2\), получаем \(f'(2) = 3*2^2-4*2+1 = 5\)
Подставляем полученные значения в уравнение касательной в точке (1) $$y = 0 + 5(x-2) = 5x-10$$
2. Уравнения касательных в точке с координатами (0;-2)
Найдем значение производной функции в точке \(x_0=0\), получаем \(f'(0) = 3*0^2-4*0+1 = 1\)
Подставляем полученные значения в уравнение касательной в точке (1) $$y = -2 + 1(x-0) = x-2$$
Ответ: уравнения касательных к графику функции \(y=(x^2+1)(x-2)\) в точках пересечения с осями координат: \(y = 5x-10\) и \(y = x-2\)