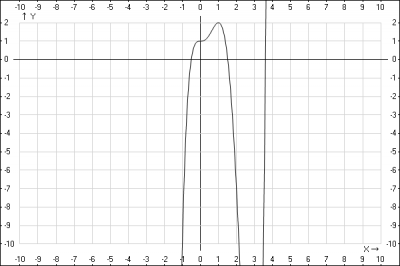
Найдем наибольшее и наименьшее значения функции \( y= x^5-5x^4+5x^3+1 \) на отрезке \( x \in [-1, 2] \).
Наибольшим, наименьшим значением функции на отрезке могут быть точки:
1. максимума,
2. минимума,
3. или значения функции на концах отрезка.
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:
1. Находим стационарные точки:
Для нахождения стационарных точек найдем первую производную и приравняем ее у нулю $$y' = ( x^5-5x^4+5x^3+1)' = 5x^4-20x^3+15x^2 $$ приравняем производную к нулю $$ y' = 5x^4-20x^3+15x^2 = 0 => $$$$ 5x^2(x^2-4x+3) = 0; \quad x = 0; \quad x=1 \quad x=3$$ функция имеет три стационарные точки.
2 Выбираем из полученных стационарных точек те, которые принадлежат заданному отрезку.
Функция \(y\) отрезке [-1, 2] имеет точку вероятного экстремума (минимума, максимума) \(x = 0; \quad x=1\).
3. Находим значения функции в стационарных точках (см п.2).
Найдем значение функции в этих точках
$$f(0)= x^5-5x^4+5x^3+1 = 1$$
$$f(1)= x^5-5x^4+5x^3+1 = 2$$
4. Находим значения функции на концах заданного отрезка:
$$f(-1)= x^5-5x^4+5x^3+1 = -10$$
$$f(2)= x^5-5x^4+5x^3+1 = -7$$
5. Из полученных значений функции (п.3 и п.4) выбираем наибольшее и наименьшее значения.
Сравниваем результаты, полученные в п.3 и п.4
Наибольшее значение выбираем из точек максимума (если есть) и значений функции на концах отрезка.
Наименьшее значение выбираем из точек минимума (если есть) и значений функции на концах отрезка.
Наибольшее значение функции на отрезке - значение функции в точке максимума \(f(1) = 2 \)
Наименьшее значение функции на отрезке - значение функции в левой границе отрезка \(f(-1) =-10 \)
Проверяем полученный результат, строим график функции: