Решение: найдем асимптоты функции \(y=\frac{4x^3-3x}{4x^2-1}\)
Асимптоты.
Вертикальная асимптота.
Вертикальная асимптота — прямая вида \(x=a\) при условии существования предела \(\lim_{x \to a}f(x) = \infty\)
Найдем областью определения функции, для дроби - знаменатель не равен нулю: \(4x^2-1 \ne 0 => x \ne \pm \frac{1}{2}\), получили область определения $$D_f=(-\infty;-\frac{1}{2}) \cup (-\frac{1}{2}; \frac{1}{2}) \cup (\frac{1}{2}; \infty)$$ Из области определения следует, что функция может иметь две вертикальные асимптоты \(x = -\frac{1}{2}; \quad x = \frac{1}{2}\). Найдем односторонние пределы и определим поведение функции в окрестности этих точек, преобразуем функцию \( \frac{4x^3-3x}{4x^2-1} = x\frac{4x^2-1-2}{4x^2-1} = x(1 - \frac{2}{4x^2-1}) \) $$ \lim_{ x \to -\frac{1}{2}-0}x(1 - \frac{2}{4x^2-1}) = +\infty $$$$ \lim_{ x \to -\frac{1}{2}+0} x(1 - \frac{2}{4x^2-1}) = -\infty $$$$ \lim_{ x \to \frac{1}{2}-0} x(1 - \frac{2}{4x^2-1}) = +\infty $$$$ \lim_{ x \to \frac{1}{2}+0} x(1 - \frac{2}{4x^2-1}) = -\infty $$
прямые \(x=-\frac{1}{2}; \quad x= \frac{1}{2}\) - вертикальные асимптоты.
Наклонная асимптота.
Наклонная асимптота — прямая вида \(y = kx+b \quad (1)\)
Для того, чтобы график функции \(y = \frac{4x^3-3x}{4x^2-1}\) при \(x \to \infty\) имел наклонную асимптота \(y = kx+b\), необходимо и достаточно, чтобы существовали два предела $$\lim_{x \to +\infty}=\frac{f(x)}{x} =k ; \quad \lim_{x \to +\infty}(f(x) - kx) = b $$ находим пределы $$ \lim_{x \to +\infty}\frac{\frac{4x^3-3x}{4x^2-1}}{x} = 1 => k= 1$$ и второй предел $$ \lim_{x \to +\infty}(\frac{4x^3-3x}{4x^2-1} - x) = \lim_{x \to +\infty}(\frac{4x^3-3x -4x^3+x }{4x^2-1} ) = 0 => b=0 $$ Подставляем в уравнение прямой (1) и получаем наклонную асимптоту $$y = x$$
Горизонтальная асимптота:
для того, чтобы существовала горизонтальная асимптота, необходимо, чтобы существовал предел $$\lim_{x \to +\infty}f(x) = b$$ найдем его $$\lim_{x \to +\infty} (\frac{4x^3-3x}{4x^2-1}) =\infty$$Получили, что график функции горизонтальную асимптоту не имеет.
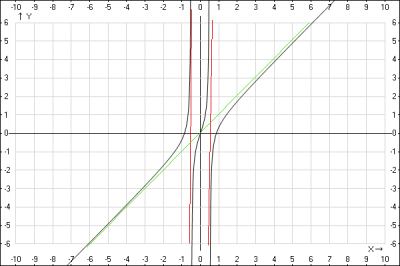
График функции:
проверяем решение, смотрим на график функции \(y=\frac{4x^3-3x}{4x^2-1}\)